Периодичность - потенциал
Cтраница 2
Наиболее характерным из условий, в которых находятся электроны в кристалле, является периодичность потенциала, отражающая особенности структуры кристаллической решетки. Учета периодичности потенциала достаточно для того, чтобы качестве н-н о описать поведение электронов в кристалле, тогда как точное решение задачи из-за огромного числа частиц вообще теряет смысл. Например, характерные черты радиоактивного ос-распада ядра можно описать с помощью модели простого потенциального барьера, хотя точный потенциал а-частицы в ядре не известен. [16]
Обратимся вновь к красителю, молекула которого изображена на стр. Распределение энергетических уровней для этого соединения, соответствующее упрощенной модели ящика с плоским дном, в которой периодичность потенциала не учитывается, представлено на рис. 82, а. В действительности электроны в такой системе находятся в периодическом поле ( см. рис. 79, а), поскольку около каждого атома имеет место некоторое падение потенциала. Вследствие этого все уровни группируются в зоны ( рис. 82, б), каждая из которых содержит 2 / 2 уровней, где / - число изображаемых двойных связей. Для рассматриваемого красителя / 3 и в каждой группе содержится по 8 уровней. Последним заполненным оказывается 4 - й уровень. Поэтому оптический переход осуществляется между 4 - м и 5 - м уровнями, лежащими в средней части нижней зоны. Сопоставление этих энергетических схем показывает, что учет периодического потенциала изменяет главным образом относительное расположение уровней, которые при этом оказываются крайними в смежных зонах ( 8 - й и 9 - й уровни), и почти не сказывается на расположении интересующих нас в данном случае средних уровней нижней зоны. Свидетельство этому - полученное Куном согласие расчетных и экспериментальных значений для длин волн, соответствующих полосам поглощения симметричных красителей. [17]
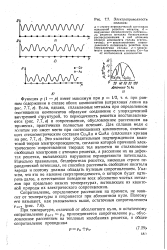 |
Электропроводность сплавов. [18] |
Если, однако, сплавляемые металлы при определенном соотношении компонентов образуют соединение с упорядоченной внутренней структурой, то периодичность решетки восстанавливается ( рис. 7.7, в) и сопротивление, обусловленное рассеянием нэ примесях, практически полностью исчезает. Это является убедительным подтверждением квантовой теории электропроводности, согласно которой причиной электрического сопротивления твердых тел является не столкновение свободных электронов с атомами решетки, а рассеяние их на дефектах решетки, вызывающих нарушение периодичности потенциала. Идеально правильная, бездефектная решетка, имеющая строго периодический потенциал, не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением. [19]
Конечно, это неправильно, хотя и трудно освободить некоторые металлы от кислорода. Но если содержание кислорода свести приблизительно до 0 01 %, то он влияет на свойства гораздо меньше, чем такое же количество ( в атомных процентах) какого-нибудь другого элемента, например железа. Этот парадокс легко понять - нарушение периодичности потенциала решетки ( которое обусловливает как изменение свойств, так и растворимость) при наличии хорошо растворимых примесей становится меньше. В этом случае оно является даже причиной хорошей растворимости. Например, на ковкость хрома кислород оказывает лишь небольшое влияние. [20]
Такая связь с импульсом светового поля, однако, слегка вводит в заблуждение. Данное квантование проистекает не из квантовой природы поля излучения. Оно обусловлено периодичностью потенциала, точнее, периодичностью модовой функции электромагнитного поля. [21]
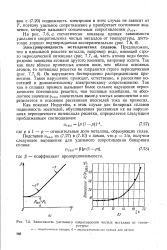 |
Зависимость удельного сопротивления чистых металлов от температуры. [22] |
Предположим, что в идеальной решетке металла, например меди, имеющей строго периодический потенциал ( рис. 7.7, а), часть атомов меди беспорядочно замещена атомами другого элемента, например золота. Он нарушается беспорядочно распределенными примесями. Такое нарушение приводит, естественно, к рассеянию носителей и дополнительному электрическому сопротивлению. Так как в сплавах примеси вызывают более сильное нарушение периодичности потенциала решетки, чем тепловые колебания, то абсолютное значение рспл значительно выше р чистых компонентов и определяется в основном рассеянием носителей тока на примесях. [23]
Несмотря на наличие сопряжения, связи все же преимущественно сохраняют характер одиночных и двойных; поэтому и межатомные расстояния в такой цепи неодинаковы. В молекуле, формула которой здесь изображена, связи, записанные как одиночные, действительно длиннее двойных связей. Периодический потенциал для сопряженной системы этой молекулы представлен на рис. 83, а. Периодичность потенциала и в этом случае приводит к группированию уровней в зоны. Но поскольку период здесь в 2 раза больше, чем для симметричного красителя с такой же длиной сопряжения ( см. рис. 79), то число уровней в каждой зоне уменьшено вдвое. Здесь 4 - й последний заполненный уровень оказывается уже верхним в своей зоне, и энергия перехода на следующий уровень сильно отличается от энергии, определяемой моделью свободных электронов. Это облегчает расчет энергетического спектра и в то же время правильно передает физическую картину, так как периодичность потенциала учитывается и тем самым отражается реальное распределение энергетических уровней, сгруппированных в зоны. [25]
Однако такая ассоциация не обязательно будет полной, и при этом не все доноры могут быть полностью окислены и не все акцепторы полностью восстановлены; изменение энергии в таком случае обозначается через ЕВ. Для достижения высокого значения электропроводности необходимо также равенство межмолекулярных расстояний внутри каждой из сегрегированных стопок. Если межмолекулярные расстояния не одинаковы, соединение скорее всего будет полупроводником. Например, в случае соли Cs2 ( TCNQ) 3 вдоль осей сегрегированных стопок TCNQ проявляется тримерная модуляция. Изменение межмолекулярных расстояний в решетке приводит к иной периодичности кристаллического потенциала и расщепляет невозмущенные зоны. [26]
Значительно сложнее обстоит дело с правой частью. Начнем с того, что рассмотрим причины, которые могут вызывать рассеяние фононов. В идеальном кристалле с упругими межатомными силами гармонические волны распространяются независимо друг от друга, не взаимодействуют и не затухают, точно так же, как электромагнитные колебания в пустоте. Это видно из того, что решение уравнения (4.6) представляет собой сумму независимых незатухающих колебаний. Эта вероятность появляется в результате возмущений - нарушений периодичности потенциала. Такими возмущениями могут быть: 1) чужеродные атомы, атомы в междуузлиях и пустые узлы ( так называемые точечные дефекты); 2) линейные дефекты - дислокации; 3) плоские дефекты - границы кристалла и зерен в поликристаллическом образце; 4) объемные дефекты - трещины, полости, поры, вкрапления другой фазы; 5) ангармоничность колебаний, обусловливающая их взаимодействие, или ( на корпускулярном языке) рассеяние фононов на фононах. [27]
Рассмотренные поверхностные состояния возникают на идеально чистой бездефектной поверхности, получить которую практически невозможно. В реальных условиях поверхностные свойства полупроводников определяются поверхностными состояниями, созданными главным образом чужеродными атомами ( молекулами) на поверхности. На рис. 8.26, в показана зонная структура полупроводника. Вертикальной прямой ВС обозначена одна из свободных его поверхностей. При такой сорбции волновые функции решетки и частицы перекрываются настолько, что частицу можно рассматривать как примесь, локально нарушающую периодичность потенциала решетки и приводящую к возникновению в запрещенной зоне поверхностного уровня. [28]
Несмотря на наличие сопряжения, связи все же преимущественно сохраняют характер одиночных и двойных; поэтому и межатомные расстояния в такой цепи неодинаковы. В молекуле, формула которой здесь изображена, связи, записанные как одиночные, действительно длиннее двойных связей. Периодический потенциал для сопряженной системы этой молекулы представлен на рис. 83, а. Периодичность потенциала и в этом случае приводит к группированию уровней в зоны. Но поскольку период здесь в 2 раза больше, чем для симметричного красителя с такой же длиной сопряжения ( см. рис. 79), то число уровней в каждой зоне уменьшено вдвое. Здесь 4 - й последний заполненный уровень оказывается уже верхним в своей зоне, и энергия перехода на следующий уровень сильно отличается от энергии, определяемой моделью свободных электронов. Это облегчает расчет энергетического спектра и в то же время правильно передает физическую картину, так как периодичность потенциала учитывается и тем самым отражается реальное распределение энергетических уровней, сгруппированных в зоны. [29]
Страницы: 1 2
