Пигфорд

Cтраница 2

Джонстона и Пигфорда [112] по изучению систем дихлорэтан-толуол, этанол-вода, ацетон-хлороформ и бензол-толуол, полученные результаты хорошо согласуются между собой в широком диапазоне изменения чисел Рейнольдса. [16]

Данные Эммерта и Пигфорда 147 ] по абсорбции и десорбции кислорода и диоксида углерода водой с добавкой ПАВ хорошо согласуются с теорией при повышенных скоростях течения воды. [17]

Ропер, Хэтч и Пигфорд [1] рассмотрели проблему химической абсорбции на примере одновременной абсорбции двух взаимодействующих между собой газов в жидкой фазе. Физическим процессом, который наводит на мысль о рассмотрении этой проблемы, является абсорбция двуокиси углерода и аммиака водой; в жидкой фазе СО2 и NH3 реагируют с образованием либо карбоната, либо карбамата аммония. Ясно, что рассматриваемый процесс не может протекать в режиме мгновенной реакции, потому что концентрация обоих реагентов на поверхности газ - жидкость конечна. Следовательно, необходимо рассмотреть только режимы медленной и бы -, строй реакции. [18]

На основании этих вычислений Пигфорд, Теп и Гаррахан заключили, что имеется общая тенденция к увеличению размера промежуточной фракции с увеличением задержки. В одном случае при большой относительной летучести величина промежуточной фракции проходит через минимум с увеличением задержки; оптимум был при задержке, отвечающей 2 % загрузки. [19]

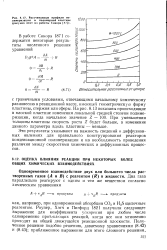Рассчитанные профили полимеризации в полимерной пластине ( рисунок взят из работы Сикора. [20]

Роупер, Хэтч и Пигфорд [82] получили следующее выражение для коэффициента ускорения при любом числе одновременно протекающих реакций, когда все они мгновенно проходят на общей движущейся реакционной плоскости. [21]

Диффузия от точечного источника в поток. [22]

Анализ Гретца был модифицирован Пигфордом [46], чтобы принять во внимание поправку на изменение вязкости и плотности с изменением температуры, когда среда нагревается или охлаждается при ламинарном течении через вертикальную трубу. Гольдман и Барретт [27] применили анализ Пигфорда при изучении массоотдачи с целью учесть изменение свойств жидкости и коэффициента диффузии с изменением концентрации диффундирующего вещества. Гольдман и Барретт сообщают данные экспериментов по растворению трубы из соли в ламинарных потоках ( 0 03 Re 140) водных растворов глицерина. [23]

В основу книги Бенедикта и Пигфорда Химическая технология ядерных материалов положены прочитанные авторами лекции по ядерной химической технологии. [24]

Вновь заметим, что формула Пигфорда в вышеприведенном виде пригодна только в случае, когда коэффициент теплоотдачи относится к входной температуре потока. [25]

Мы остановились на работах Слиса [79] и Пигфорда [81], 1тобы пояснить те трудности, которые имеются на пути создания еории возникновения неоднородностей в кипящем слое. [26]

Было показано 16, что при обсуждении уравнения Пигфорда и Барона Шапелье использовал аналогичные предпосылки. Отмечено также7 существование иных типов волн, чем описываемые в более ранних уравнениях 5 в, но не указано, что обнаруженные в решениях дополнительные виды колебаний являются поперечными волнами и что они не вызывают флуктуации порозности. [27]

Уравнение (2.17) было использовано Оркатом, Дэвидсоном и Пигфордом [79] для оценки эквивалентного диаметра пузырей Dc по наблюденной зависимости высоты слоя от скорости U при псевдоожижении воздухом слоя частиц катализатора. [28]

Экспериментальные данные хорошо совпадают с результатами расчета по уравнениям Кента и Пигфорда. При большой скорости конденсации число единиц переноса массы не зависит от сопротивления; массопередаче; поэтому величина БПМ может быть определена по уравнению Релея при условии, что состав элементарного объема конденсирующейся жидкости равновесен составу пара. [29]

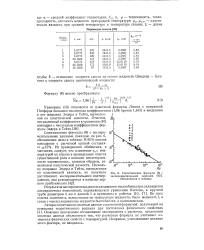Сопоставление формулы ( 8 с. [30]

Страницы: 1 2 3 4