Пигфорд
Cтраница 3
Уравнение ( 10) отличается от известной формулы Левека с поправкой Пигфорда большим численным коэффициентом ( 1 86 против 1 615) и введением в нее поправки Зидера и Тейта, вычислен - j ной по пластической вязкости. [31]
Мерфри) от общей эффективности всего абсорбера, найденная Маршаллом и Пигфордом. [33]
Недавно Бриан и Биверстек [9] заявили, что некоторые результаты Эммерта и Пигфорда [10] могут быть объяснены по предложенной ими модели абсорбции, сопровождающейся двухстадийной химической реакцией. При этом необходимо, чтобы константа скорости / JXIY была намного меньше, чем & хш - Имея в виду ионный характер реакции ( XIV), это обстоятельство представляется маловероятным. [34]
В отличив от них Шен и Джонетон [316], Мэй [209], Ван-Деемтер [342], Оркут, Дэвидсон и Пигфорд [235] придерживаются противоположной точки зрения, совпадающей с концепцией Дэвидсона и Харрисона. [35]
Единственными экспериментальными данными о скорости обновления поверхности при газовой абсорбции являются, вероятно, результаты измерений Лэмба, Спрингера и Пигфорда [88, 159], которые использовали мост для определения полного сопротивления границы раздела. [37]
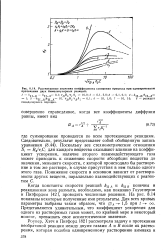 |
Рассчитанные значения коэффициента ускорения процесса при одновременном протекании двух бимолекулярных реакций. [38] |
Когда константы скорости реакций kn A и kllB конечны и реакционная зона размыта, необходимо, как показано Гоуэтлером и Пигфордом [42], проводить численные решения. На рис. 8.14 показаны некоторые полученные ими результаты. [39]
По предложению Риппина и Лемба, изменения в условиях питания ректификационной колонны должны непрерывно регистрироваться и передаваться аналоговой вычислительной машине, которая использует уравнения Лемба и Пигфорда для расчета и выполняет корректирующее воздействие с такой скоростью, что составы продуктов остаются неизменными. Риппин и Лемб моделировали такую колонну, используя аналоговую машину, и применили к ней свой метод регулирования; при этом было показано, что в случае заметных и быстрых изменений в условиях ввода исходной смеси составы продуктов изменяются незначительно. [40]
Блох и Кичкина, Джиффен и Мурашев) удовлетворительно укладываются на аппроксимирующие линии, опыты в [2.62] - хуже, две точки из пяти, а в опытах Пигфорда и Пайла - одна точка из двух. Два остальных опыта выпадают и, видимо, не учитывались при обработке. Наибольшим количеством точек представлены опыты Блоха и Кичкиной - 16 точек, полученных с использованием форсунок одной конструкции. Анализ обобщения опытных данных в [2.62], так же как и выводы других авторов, приводит к заключению о необходимости осторожного использования таких зависимостей. Вопрос о влиянии особенностей конструкции форсунки - которое не может быть простым образом учтено в обобщенном соотношении, должен решаться, видимо, путем испытания образцов распылителей или использования геометрически подобных форсунок. [41]
Эта система с граничными условиями (3.6) - (3.7) представляет собой нелинейную краевую задачу. Пигфорда приведено пять рисунков, иллюстрирующих зависимость одного из коэффициентов ускорения от R для ряда сочетаний параметров; практическое использование этих результатов связано с большими трудностями. [42]
Результаты, полученные Пигфордом в [129] при е2 0, представлены на рис. 5.1 и 5.2. Они дают достаточно близкие к точным, хотя и несколько завышенные значения числа Шервуда. [43]
Анализ Гретца был модифицирован Пигфордом [46], чтобы принять во внимание поправку на изменение вязкости и плотности с изменением температуры, когда среда нагревается или охлаждается при ламинарном течении через вертикальную трубу. Гольдман и Барретт [27] применили анализ Пигфорда при изучении массоотдачи с целью учесть изменение свойств жидкости и коэффициента диффузии с изменением концентрации диффундирующего вещества. Гольдман и Барретт сообщают данные экспериментов по растворению трубы из соли в ламинарных потоках ( 0 03 Re 140) водных растворов глицерина. [44]
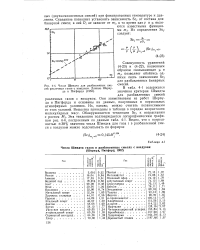 |
Числа Шмидта для разбавленных смесей различных газов с воздухом. Данные Шервуда и Пигфо рда ( 1952. [45] |
Страницы: 1 2 3 4