Плоскость - параллелограмм
Cтраница 3
Плоскости, проходящие соответственно через начало координат и скорости vl и ov назовем Р и Q. Плоскость Р, очевидно, перпендикулярна к вектору О, a Q к G2; следовательно, каждая из этих плоскостей перпендикулярна к плоскости параллелограмма, построенного на векторах О, G2; линия их пересечения ОА также перпендикулярна к плоскости этого параллелограмма, а значит, и к постоянному направлению вектора G. Итак, оказывается, что три плоскости, Р, Q и плоскость, проведенная через точку О перпендикулярно к кинетическому моменту G, пересекаются по одной прямой. Другими словами, геометрическим местом прямых встречи плоскостей Р и Q, проведенных через начало координат и скорости движущихся частиц, служит неизменяемая плоскостей Лапласа. [31]
Приложим оба эти вектора к одной точке О. Векторное произведение [ F4, F2 ] определяется как свободный вектор, равный по величине площади параллелограмма, построенного на векторах F4 и F2, направленный по нормали к плоскости параллелограмма в сторону, откуда вращение от F. [32]
Условие равенства длин измерительного и сравнительного пучков в идеализированном МЦИ удовлетворяется формой параллелограмма в плоском интерферометре ( фиг. Кроме того, при отражении от плоского зеркала падающий пучок, отраженный пучок и нормаль к поверхности зеркала в точке отражения фг лежат в одной плоскости, которая в данном случае является плоскостью параллелограмма плоского интерферометра. Плоский интерферометр, описанный в разд. В общем случае геометрическое место точек отражения ( 2 - представляет собой симметричный эллипсоид вращения, показанный на фиг. [33]
Изображенный на рис. 5 параллелограмм характеризуется, помимо величины и направления вращения, еще и положением в пространстве. Для наглядности это положение обычно характеризуется нормалью к плоскости параллелограмма. При этом по общей договоренности выбирают то направление нормали, которое образует с направлением момента вращения правовинтовую систему. Тогда векторным изображением момента будет направленная по этой нормали стрелка, длина которой равна величине момента. IV, § 23, мы подробно остановимся на таком способе изображения и на различии между аксиальными и полярными векторами. [34]
А и В, а с - единичный вектор, перпендикулярный к А и В, таким образом, что А, В и с образуют правую систему. Если пальцы правой руки направлены от А к В, то большой палец указывает направление с. Длина А х В численно равна площади параллелограмма со сторонами А и В, а направление перпендикулярно плоскости параллелограмма. [35]
На рис. 50 поверхность заняла необходимое для решения задачи положение: ребра ее стали горизонтально проецирующими. В таком положении поверхности горизонтальная проекция abed искомого сечения совпадает с горизонтальной проекцией pqst призматической поверхности. Большая ось эллипса по положению и направлению служит горизонтальной проекцией тп горизонтали плоскости параллелограмма. Обычными построениями определяем величину угла а. [36]
Тогда гр означает вектор, численно равный площади параллелограмма и перпендикулярный его плоскости. Для того чтобы задать направление М однозначно, надо условиться о способе обхода контура параллелограмма. Будем всегда обходить контур начиная с первого векторного сомножителя, в данном случае начиная с г. Тогда положительной считается та сторона плоскости параллелограмма, в которой обход производится против часовой стрелки. Вектор М направлен по нормали к положительной стороне плоскости. [37]
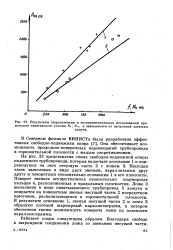 |
Результаты теоретических и экспериментальных исследований продольного сдвигающего усилия No, Рпр в зависимости от начальной затяжки. [38] |
Несущая часть выполнена в виде двух звеньев, параллельных друг ДРУГУ и поворотных относительно основания 1 в его плоскости. Поворот звеньев осуществляется относительно шарнирных пальцев 4, расположенных в продольных плоскостях. Ложе 3 выполнено в виде охватывающего трубопровод 5 хомута и опирается на поворотные звенья несущей части 2 посредством крестовин, располагающихся в горизонтальной плоскости. В результате основание 1, звенья несущей части 2 и ложе 3 образуют плоский шарнирный параллелограмм, в котором обеспечена также возможность поворота ложа из плоскости параллелограмма. [39]
Вместо этого построения можно применить еще следующее. Через конец первого вектора а проведем второй вектор b так, чтобы его начальная точка совпала с концом первого, и дополним полученную ломаную линию ABD из двух колен до параллелограмма ABDC. Этот второй способ построения будет использован ниже, в § 13, при изображении момента силы через векторное произведение. Найдем площадь параллелограмма ABDC и условимся изображать ее символически отрезком с, взяв для длины его столько каких-нибудь линейных единиц, сколько в площади параллелограмма содержится квадратных единий, и построив его с положительной стороны параллелограмма перпендикулярно к плоскости параллелограмма. Наложим на образованные вышеуказанным способом отрезки с еще новое условие, что их можно геометрически складывать; это новое условие в противоречии с определением отрезка с не находится, и ниже в этом же параграфе смысл таких сложений будет выяснен. Вместе с тем будет также выяснено, что действие получения отрезка с из векторов а и b обладает характерными свойствами умножения. [40]
Страницы: 1 2 3