Плоскость - частное положение
Cтраница 2
Задание на чертеже прямых и плоскостей частного положения значительно упрощает решение задач и делает его выполнимым при помощи простейших графических построений. [16]
Решение оказывается простым, если прямая пересекает плоскость частного положения - проецирующую или плоскость уровня. [17]
Плоскости уровня и проецирующие плоскости называют также плоскостями частного положения. [18]
Во втором и третьем случаях плоскости называют плоскостями частного положения. [19]
 |
Взаимное положение двух прямых Изображение плоскости на комплексном чертеже. [20] |
Как и в случае с прямыми линиями различают плоскости общего и частного положения. [21]
При таком режиме построения выполняют в одной из плоскостей частного положения, параллельной соответствующей плоскости проекций. В этом случае построение изображения пользователем на одной из проекций автоматически сопровождается практически синхронным построением проекции изображения на остальных плоскостях проекций. В этом режиме с помощью курсора построены фронтальные проекции вертикального отрезка и автоматически - его профильная проекция и аксонометрия, затем на рис. 499 6 -наклонного отрезка и автоматически - его горизонтальная проекция и аксонометрия. Введен режим тс, и построена горизонтальная проекция отрезка, перпендикулярного плоскости Л2, и автоматически - его профильная проекция и аксонометрия. На рисунках текущие построения показаны тонкими линиями, ранее выполненные - толстыми. Эти графические отличия могут быть и запрограммированы. [22]
В зависимости от положения плоскости относительно плоскостей проекций различают плоскости общего и частного положения. Плоскостью общего положения называется плоскость, наклоненная ко всем трем плоскостям проекций под произвольными углами. Такая плоскость на чертеже имеет три следа и три точки схода следов. Все ее следы наклонены к осям проекций. [23]
Если хотя бы одна из двух пересекающихся плоскостей является плоскостью частного положения, то одна проекция линии пересечения задана. Например, при построении линии пересечения треугольника SAB общего положения и прямоугольника CDEF, расположенного перпендикулярно плоскости V ( рис. 242), задана фронтальная проекция линии пересечения. Она представляет собой отрезок т п - общий для фронтальных проекций фигур. Через точки т и п проводят линии связи и на пересечении их с горизонтальными проекциями сторон SA и SB треугольника получают точки тип. Отрезок тп является горизонтальной проекцией линии пересечения заданных фигур. [24]
Рассмотрим, можно ли применить в качестве вспомогательных секущих поверхностей плоскости частного положения. Горизонтальные плоскости уровня пересекают цилиндрическую поверхность по эллипсам. Горизонтально - и фронтально-проецирующие плоскости, проходящие через вершину конической поверхности, пересекают цилиндрическую поверхность также по эллипсам. Значит эти плоскости не следует использовать в качестве вспомогательных секущих поверхностей, так как они дают сложные для построения на чертеже линии. [25]
Плоскости, параллельные или перпендикулярные ос-новным плоскостям проекций, называются плоскостями частного положения. Соответственно, плоскости частного положения могут быть плоскостями уровня и проецирующими. Плоскости уровня являются одновременно и проецирующими соответствующих плоскостей. [26]
Аналогично решают задачи и в том случае, когда на чертеже даны плоскости частного положения. [27]
Плоскости уровня и проецирующие плоскости в отличие от плоскости общего положения называются плоскостями частного положения. [28]
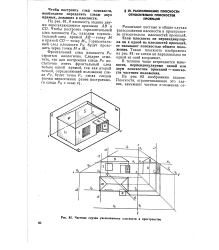 |
Частные случаи расположении плоскости в пространстве. [29] |
В технике чаще встречаются плоскости, перпендикулярные одной или двум плоскостям проекций - плоскости частного положения. [30]
Страницы: 1 2 3