Плоскость - годограф
Cтраница 2
Характеристиками на плоскости годографа скорости являются эпициклоиды, получающиеся при качении без сколь: жения круга диаметром Umax-юкр - по окружности радиуса гкр - При качении и одну сторону получаются характеристики одного семейства, при качении в другую сторону - характеристики другого семейства. [16]
Недостаток использования плоскости годографа для описания автомодельных решений связан с возможной неоднолистностью обратного отображения, при которой начало координат является точкой ветвления. [17]
Наряду с плоскостью годографа uv удобно также рассматривать плоскость w, aigw. В этой плоскости граница F ( G) состоит из двух отрезков оси w 0 и двух кривых - образов верхней и нижней сторон профиля. [18]
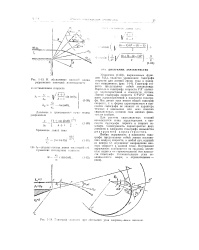 |
К объяснению плоско.. волны разрежения конечной интенсивное.| Годограф скорости при обтекании угла сиерхзвчловым потоком. [19] |
Любая окружность в плоскости годографа представляет собой линию постоянного модуля скорости, а любой луч, идущий из центра О, определяет направление вектора скорости в данной точке. [20]
Если уравнение в плоскости годографа некоторой заменой переменных может быть преобразовано в уравнение Лапласа, как это имеет место в случае закона В. В. Соколовского и закона, предложенного С. В. Панько, к решению задачи в плоскости годографа применим весь аппарат теории аналитических функций, так что решение, в принципе, получается весьма просто. Не останавливаясь на этом более подробно, укажем лишь работы [12, 88. 165, 227], в которых рассматриваются такие решения. [21]
Ударная поляра в плоскости годографа. [22]
Любая окружность в плоскости годографа представляет собой линию постоянного модуля скорости, а любой луч, идущий из центра О, определяет направление вектора скорости в данной точке. [23]
Ударная поляра в плоскости годографа. [24]
Характеристики (18.15) в плоскости годографа Г и Г являются отображениями характеристик 0 и С в физической плоскости. [25]
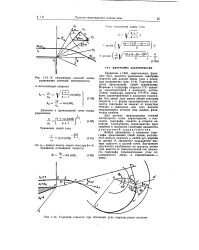 |
К объяснению плоской волны разрежения конечной интенсивности.| Годограф скорости при обтекании угла сверхзвковым потоком. [26] |
Любая окружность в плоскости годографа представляет собой линию постоянного модуля скорости, а любой луч, идущий из центра О, определяет направление вектора скорости в данной точке. [27]
Скачок уплотнения в плоскости годографа изображается кривыми 1, 2 ( до и после скачка): и i ( s), v i ( s), i. [28]
Ох, в плоскости годографа скорости, то нелинейные в физической плоскости ( х, у) уравнения газовой динамики становятся в плоскости годографа скорости ( w, 9) линейными. [29]
При изучении в плоскости годографа задач, связанных с обтеканием профиля, возникает необходимость иметь представление решения в виде суммы регулярной и сингулярных компонент. Эта форма должна соответствовать асимптотическому разложению вблизи образа бесконечно удаленной точки. Как уже упоминалось, отображение окрестности бесконечно удаленной точки течения с ненулевой циркуляцией в плоскость годографа взаимно однозначно. [30]
Страницы: 1 2 3 4