Срединная плоскость

Cтраница 2

Перемещения точек срединной плоскости в направлении осей Ох, Оу ( продольные перемещения) полагаются малыми величинами в сравнении с прогибом и в силу этого не учитываются. [16]

Линии пересечения срединной плоскости с боковой поверхностью образуют контур пластины. [17]

Положение точек срединной плоскости 50 в ее недеформирован-ном состоянии определяется вектором р, а положение любой точки В пластины до деформирования определяет вектор ( см. рис. 16 2) г-р zm, где. [18]

Нормаль к срединной плоскости в каждой точке поперечного сечения пластины может иметь пять перемещений. [19]

Рассматриваемый элемент срединной плоскости находится в равновесии, следовательно, должны выполняться шесть условий равновесия: три уравнения проекций на координатные оси и три уравнения моментов относительно этих осей. [20]

Положение точек срединной плоскости S0 в ее недеформированном состоянии определяется вектором р, а положение любой точки В пластины до деформирования определяет вектор ( см. рис. 16.2) г - р г / и, где г - расстояние до точки В от срединной плоскости. [21]

Линии пересечения срединной плоскости с боковой поверхностью образуют контур пластины. [22]

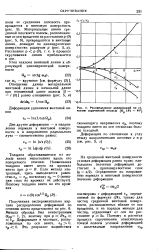Распределение деформаций по сечению скрученной полосы ( В ( К 46. [23]

Материальные линнн срединной плоскости полосы, расположенные от оси вращения иа расстоянии р ( 0) ( рнс. [24]

Если прогиб срединной плоскости пластинки мал по сравнению с толщиной пластинки, то имеют место следующие допущения: 1) нормаль к срединной плоскости до изгиба переходит в нормаль к срединной плоскости после изгиба; 2) компонент тензора напряжений 0зз кал по сравнению с другими компонентами тензора напряжений; 3) при изгибе пластинки срединная плоскость не деформируется. [25]

Если прогиб срединной плоскости пластинки мал по сравнению с толщиной пластинки, то имеют место следующие допущения: 1) нормаль к срединной плоскости до изгиба переходит в нормаль к срединной плоскости после изгиба; 2) компонент тензора напряжений сгзз кал по сравнению с другими компонентами тензора напряжений; 3) при изгибе пластинки срединная плоскость не деформируется. [26]

Пластина характеризуется срединной плоскостью, которая делит ее пополам по толщине. Для оболочки этим геометрическим элементом является срединная поверхность. [27]

При изгибе пластинки срединная плоскость превращается в изогнутую срединную поверхность пластинки. [28]

При этом в срединной плоскости отсутствуют деформации растяжения ( сжатия) и сдвига, то есть она является нейтральной. Расчет пластин на основе рассмотренных выше гипотез достаточно прост и позволяет получать доступные для инженерной практики решения. Эти решения и будут рассмотрены в дальнейшем. [29]

В центральной зоне срединной плоскости как в упруго-мягкой ( рис. 4.53, д) напряжения распределены равномерно или почти равномерно. Зато на участках, близких к поверхности пластин, имеются существенные градиенты напряжений, причем, тем большие, чем тоньше прослойка. Интересно отметить, что в середине, а в упруго-мягкой, наоборот, - меньше. [30]

Страницы: 1 2 3 4