Диагональная плоскость

Cтраница 1

Оптическая схема интерференционного микроскопа МИИ-4. [1]

Диагональная плоскость одной из этих призм посеребрена, что делает призму полупрозрачной. Это необходимо для разделения пучка света на два. Один пучок проходит через призму без преломления, а затем, пройдя через объектив 12, попадает на зеркало 13, служащее образцовой плоскостью. [2]

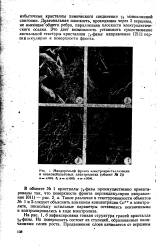Микрорельеф фронга электрокристалЛизацнн в ниакокобальтовых электролитах ( объект № 2 1. [3]

Диагональная плоскость, проходящая через 3 вершины, не имеющие общего, ребра, параллельна плоскости электролитического осадка. Это дает возможность установить существование аксиальной текстуры кристаллов 72-фазы: направление [211] пер-пен шкулярно к поверхности фронта. [4]

Диагональная плоскость, проходящая через начало координат, не отсекает отрезков осей. Следует заметить, что миллеровские индексы даются не отдельным определенным плоскостям кристаллической решетки, а целой серии плоскостей. Плоскости могут быть сдвинуты параллельно, так что для обозначения могут использоваться, например, такие отрезки, как 1, - 1, со. [5]

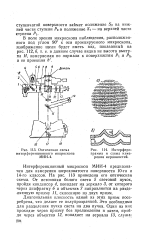Оптическая схема. [6]

Диагональная плоскость одной из этих призм посеребрена, что делает ее полупрозрачной. Это необходимо для разделения пучка света на два пучка. [7]

Диагональная плоскость прямоугольного параллелепипеда и лежащая в ней диагональ d образуют с одной и той же боковой гранью соответственно углы ир. [8]

Для диагональной плоскости ( заштрихована, фиг. OY и OZ имеются равные отрезки, а по отношению к оси ОХ плоскость параллельна. [9]

Площадь диагональной плоскости куба равна S. [10]

Каждая из диагональных плоскостей делит октаэдр на две пирамиды с квадратными основаниями. Куб и октаэдр имеют одинаковое число ребер. В октаэдр может быть вписан куб, а в куб - октаэдр так, что вершины одного многогранника совпадут с центрами граней другого. Такие многогранники называются взаимно соответствующими. [11]

Составьте уравнение диагональной плоскости, проходящей через вершины А и В, если точка О ( 1 / 2; 1 / 2; 1 / 2) - центр куба. [12]

Почему на диагональной плоскости призмы Волластона происходит расщепление падающего луча. [13]

Сечение AMND и диагональная плоскость ASC разбивают денную пирамиду на четыре части. ABCD, то ее объем равен и / 4, где v - объем данной пирамиды. [14]

На эту же диагональную плоскость попадают лучи от фотометрической лампы 6, проходящие через бихроматический ( не регулируемый) фильтр 7 и отразившиеся от зеркальной части диагональной поверхности оптического кубика. Таким образом, в окуляре глаз видит два поля сравнения ( фиг. [15]

Страницы: 1 2 3 4