Плотность - звезда
Cтраница 1
Плотность звезды определяется равновесием между силой тяжести и силой давления вещества звезды. Для того чтобы звезда сжалась, давление должно уменьшиться. Очень сильное уменьшение давления могло бы произойти при образовании нейтронного вещества, когда протоны и электроны превращаются в нейтроны. [1]
 |
Аккреция на ось симметрии звезд, движущихся первоначально под углом в. [2] |
Следует ожидать, что плотность звезд на наветренной стороне оси будет меньше. Это происходит потому, что звезды, отклоненные к оси, будут иметь скорость v f, а при максвелловском распределении число звезд с такими скоростями мало. Подобный анализ показывает, что с наветренной стороны оси плотность звезд, находящихся на расстоянии а от звезды, определяется соотношением (17.20), в котором vt следует заменить на - vt, что следует из симметрии задачи. [3]
 |
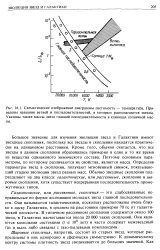
Свойства компактных сферических звездных систем. [4] |
Это соотношение означает, что столкновения становятся преимущественно разрушительными, когда плотность звезд столь высока, что звезды, расположенные вдоль радиуса скопления, окажутся вплотную друг к другу. [5]
Электрон-нейтринным взаимодействием обусловлены и другие процессы, эффективность которых зависит от температуры и плотности звезд. [6]
Из подраздела 6 ( см. выше) нам известно, что большое положительное значение и обусловлено, скорее всего, присутствием одной-единственной звезды вблизи точки О и не зависит от плотности звезд в других местах; распределение случайной величины U при очень больших и ведет себя как распределение величины притяжения ближайшей звезды. [7]
При усреднении вдоль луча зрения, естественно, большой вес имеют многочисленные звезды с низкими скоростями, относительно удаленные от центра. Если плотность звезд при приближении к центру резко возрастает, то из теоремы вириала и простой политропной модели следует, что скорости звезд должны достигать многих сотен и даже тысяч километров в секунду. Некоторые ядра галактик имеют такой резкий центральный пик светимости, что появляется возможность более глубокого проникновения в глубь этих ядер. Радиогалактика М87 представляет собой один из наиболее изученных и характерных в этом отношении примеров. Эта гигантская эллиптическая галактика имеет в оптике цепочку расположенных на одной линии горячих пятен, выходящих из ее ядра подобно струйному выбросу. Само ядро ( Dressier, 1980) представляет собой, по-видимому, звездное скопление, испускающее сравнительно немного ( 20 %) нетеплового излучения. Известна только верхняя граница радиуса ядра, но спекл-интерферометрия дает для него возможное значение & 2 пс. Дисперсия скоростей звезд в центре составляет, 600 км / с, но, возможно, ее значение ближе к 350 км / с. При г - 0 она может сильно возрастать, в отличие от дисперсии скоростей в центре изотермической или простой фоккер-планковской модели ( гл. Если такое возрастание будет достоверно установлено, оно может указывать на присутствие внутри ядра массивного объекта или на сильную анизотропию скоростей в центре. В настоящее врем имеющихся наблюдений недостаточно для выбора определенной модели; этот вопрос имеет первостепенное значение. [8]
Шаровые скопления, напротив, состоят из старых звезд, которые распределены в них однородно и сферически симметрично. К динамическому центру системы плотность звезд увеличивается до больших значений. [10]
Звезды, находящиеся на этих орбитах и пересекающие поверхность конуса с раствором на расстоянии от а до а da от звезды массы mt, должны были выйти из цилиндрической оболочки, находящейся иа расстоянии от 5 до 5 us от оси. Нам нужно найти соотношение между плотностью звезд, входящих в конус, и плотностью звезд, проходящих через цилиндр на расстоянии 5 от оси. [11]
Центром Галактики считается сферическое скопление звезд, диаметр которого равен 5000 световых лет и которое интенсивно излучает радиоволны. Концентрация звезд в центре в два или три раза превышает плотность звезд в непосредственной близости от Солнечной системы. Из центра Галактики выходят две нити, расходящиеся по спирали в одном направлении и в одной плоскости. Солнечная система находится на одной из этих спиральных нитей и обращается вокруг центра Галактики со скоростью 250 км / сек и с периодом, равным 200 млн. лет или одному галактическому году. [12]
Существуют и другие критерии, которыми можно воспользоваться, подходя к проблеме о том, конечен или бесконечен звездный мир. Следовательно, если бы такие сферические оболочки простирались до бесконечности, а плотность звезд оставалась при этом приблизительно постоянной, то глаз видел бы яркую освещенность во всех направлениях. Одно время думали, что этот аргумент существенно ослабляется замечанием, что пространство не вполне пусто: в нем присутствуют атомы и частички пыли повсеместно, преимущественно с малой плотностью, но иногда в форме концентрированных облаков. Последние поглощают и рассеивают проходящие через них световые лучи, тем самым затуманивая и затемняя звезды. [13]
Такой ответ несовместим с Ньютоновой теорией. Последняя скорее требует, чтобы мир имел некоторого рода середину, в которой плотность звезд была бы максимальной, и чтобы, начиная от этой середины, звездная плотность уменьшалась и, наконец, далеко во вне уступила бы место бесконечной пустоте. [14]
Звезды, находящиеся на этих орбитах и пересекающие поверхность конуса с раствором на расстоянии от а до а da от звезды массы mt, должны были выйти из цилиндрической оболочки, находящейся иа расстоянии от 5 до 5 us от оси. Нам нужно найти соотношение между плотностью звезд, входящих в конус, и плотностью звезд, проходящих через цилиндр на расстоянии 5 от оси. [15]
Страницы: 1 2