Плотность - распределение - вероятность
Cтраница 1
Плотность распределения вероятностей, очевидно, есть предел, к которому стремится отношение вероятности попадания в интервал к величине интервала при неограниченном приближении верхней границы интервала к нижней. [1]
Плотность распределения вероятности имеет вид f ( t) dF / dt aV 1 ехр ( - А. [2]
 |
Определение плотности вероятности. [3] |
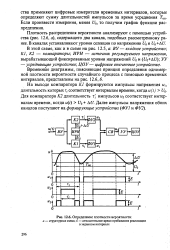
Плотность распределения вероятности анализируют с помощью устройства ( рис. 12.6, а), содержащего два канала, подобных рассмотренному ранее. [4]
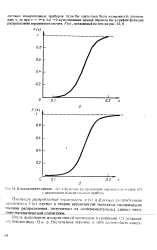 |
Кумулятивная кривая ( а и функция распределения вероятности отсчета ( б у аналогового измерительного прибора. [5] |
Плотность распределения вероятности р ( х) я функция распределения вероятности F ( x) служат в теории вероятностей моделями эмпирических законов распределения, получаемых из экспериментальных данных мето-дзми математической статистики. [6]
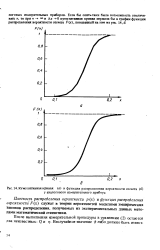 |
Кумулятивная кривая ( а и функция распределения вероятности отсчета ( б у аналогового измерительного прибора. [7] |
Плотность распределения вероятности р ( х) и функция распределения вероятности F ( x) служат в теории вероятностей моделями эмпирических законов распределения, получаемых из экспериментальных данных методами математической статистики. [8]
Плотность распределения вероятностей f ( t) характеризует распределение свойств материала. [9]
Плотность распределения вероятностей для газа в целом представляет произведение величин рг, каждая из которых зависит от координат и импульсов только одной частицы. [10]
Плотность распределения вероятностей р ( рж, ру, рг, pf, q), как мы видим, распадается на произведение двух независимых сомножителей, один из которых определяется составляющими импульса молекулы рх, ру, рг, другой - остальными обобщенными импульсами и координатами. Такой вид функции р является следствием разделения соответствующих переменных в выражении для энергии ( IV. [11]
Плотность распределения вероятностей равна 1 / К и не зависит от координат. [12]
Плотность распределения вероятностей р ( г), как правило, нельзя получить в замкнутой форме, так как интеграл, входящий в уравнение (16.62), может быть вычислен лишь в редких случаях. [13]
Плотность распределения вероятности по определению есть производная от функции распределения по случайной переменной. [14]
Плотность распределения вероятностей гармонического ригна-ла (2.7) вычисляется следующим образом. [15]
Страницы: 1 2 3 4