Плотность - распределение - вероятность
Cтраница 3
Функции и плотности распределения вероятностей наиболее полно характеризуют случайные процессы. Однако на практике нередко для оценки свойств этих процессов достаточно знать их характеристики. [31]
Требуется восстановить плотность распределения вероятностей. [32]
Вот пример плотностей распределения вероятности, расстояние между которыми велико, в то время как соответствующие функции распределения различаются на малую величину. [33]
Необходимость оценивания тяжело-хвостовых плотностей распределения вероятности ( ТТР) возникает во многих прикладных областях. Длины передаваемых по Интернету файлов, размеры страховок при катастрофах, наблюдаемые низкие или высокие температуры, сильные ветры, концентрации редких полезных ископаемых могут быть описаны тяжело-хвостовыми распределениями. [34]
Если функция плотности распределения вероятностей погрешности испытаний может быть аппроксимирована функцией Иордана ( разд. [35]
Выражение (5.116) определяет плотность распределения вероятностей огибающей сигнала на выходе устройства объединения при автовыборе. [36]
Таким образом, плотность распределения вероятностей Ф / г ( t) может быть вычислена как отношение скорости вывода частиц из / Е - Й ступени каскада к величине импульса. [37]
Функция распределения или плотность распределения вероятностей являются наиболее полными характеристиками случайных величин. Однако во многих задачах практики оказывается трудно или даже невозможно полностью описать функцию распределения вероятностей. [38]
При циклическом режиме плотность распределения вероятности подчиняется нормально-логарифмическому закону. [39]
Уравнение (5.37) дает плотность распределения вероятности для канонического ансамбля, изображающего систему при термодинамическом равновесии. [40]
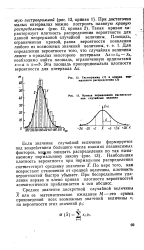 |
Гистограмма ( / и кривая нормального распределения ( 2.| Кривая нормального распределения случайных величии. [41] |
Такая кривая характеризует плотность распределения вероятности для данной непрерывной случайной величины. [42]
ПЛОТНОСТЬ ВЕРОЯТНОСТИ, плотность распределения вероятностей - производная функции распределения, отвечающей абсолютно непрерывной вероятностной мере. [43]
Предположим, что плотность распределения вероятностей р ( х 9) дифференцируема по вектору в под знаком интеграла. [44]
Отметим, что плотность распределения вероятностей определена с точностью до ее изменения на произвольном множестве меры Лебега нуль, и, в частности, можно считать, что плотность задана ц-почти всюду. [45]
Страницы: 1 2 3 4