Плотность - вероятность - нахождение - частица
Cтраница 1
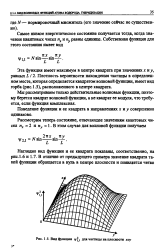 |
Вид функции /., для частицы на плоскости хоу. [1] |
Плотность вероятности нахождения частицы в определенном месте, которая определяется квадратом волновой функции, имеет вид горба ( рис. 1.5), расположенного в центре квадрата. [2]
Показать, что плотность вероятности нахождения частицы определяется только координатной ф-функцией. [3]
I Е2 I2 есть плотность вероятности нахождения частицы в данной точке пространства. [4]
Временная компонента вектора тока равна плотности вероятности нахождения частицы в точке аз в момент времени х, а его пространственные компоненты являются компонентами трехмерного вектора потока вероятности. [5]
Рассмотрим далее наряду с понятием плотности вероятности нахождения частицы в различных точках пространства и такое понятие, как плотность потока вероятности. [6]
В каких точках интервала 0 х I плотность вероятности нахождения частицы имеет экстремальные значения. [7]
Левая часть (23.15) есть производная по времени от плотности вероятности нахождения частицы вблизи некоторой точки пространства. Проинтегрируем (23.15) по всему объему, в котором может находиться частица. Если этот объем имеет конечные размеры, то за его пределами г э и - ф должны обращаться в нуль. [8]
Это уравнение имеет наглядный физический смысл: о2 есть плотность вероятности нахождения частицы в том или ином месте пространства ( ЧМ2 - я3); ySfm - p / m есть классическая скорость v частицы. Поэтому уравнение ( 17 11) есть не что иное, как уравнение непрерывности, показывающее, что плотность вероятности перемещается по законам классической механики с клас сической скоростью у в каждой точке. [9]
Это уравнение имеет наглядный физический смысл: а2 есть плотность вероятности нахождения частицы в том или ином месте пространства ( Ф 2 a2); VS / m р / т есть классическая скорость v частицы. Поэтому уравнение (17.11) есть не что иное, как уравнение непрерывности, показывающее, что плотность вероятности перемещается по законам классической механики с классической скоростью v в каждой точке. [10]
Это уравнение имеет наглядный физический смысл: а2 есть плотность вероятности нахождения частицы в том или ином месте пространства ( Ф 2 a2); VS / m р / га есть классическая скорость v частицы. Поэтому уравнение (17.11) есть не что иное, как уравнение непрерывности, показывающее, что плотность вероятности перемещается по законам классической механики с классической скоростью v в каждой точке. [11]
Определить, в каких точках интервала ( 0л СО плотность вероятности нахождения частицы имеет максимальное и минимальное значения. [12]
В этом уравнении - так называемая волновая функция, квадрат которой выражает плотность вероятности нахождения частицы в данной точке пространства. [13]
В этом уравнении ib - так называемая волновая функция, квадрат которой выражает плотность вероятности нахождения частицы в данной точке пространства. [14]
О Сдвиг локализации волновой функции Фп ( ж) избранного гг-го состояния ( управление плотностью вероятности нахождения частицы посредством изменения спектрального весового множителя сп): например, можно прижать функцию к началу координат, см. рис. 2.1. Вместе со сдвигами уровней Еп, изменения сп образуют полный набор произвольных трансформаций потенциалов. Оказывается, можно понять, как преобразуется при этом каждая пучность функции под действием простейших блоков потенциальных возмущений. При этом все другие состояния как бы отшатываются в противоположную сторону, происходит сепарация избранного состояния рис. 2.1, 2.2. Это представляет собой важный элемент волновой грамоты, долго остававшийся незамеченным со времени создания квантовой механики. [15]
Страницы: 1 2