Плотность - вероятность - нахождение - электрон
Cтраница 1
Плотность вероятности нахождения электрона около обоих ядер должна быть одинакова. [1]
Плотность вероятности нахождения электрона на ядре равна нулю; единственным исключением являются s - орбитали. Это обстоятельство, как мы увидим впоследствии, имеет очень важное значение для радиоспектроскопии. [2]
 |
Бесконечно тонкий сферический слой на расстоянии г ог ядра. [3] |
Она определяет плотность вероятности нахождения электрона в бесконечно тонком шаровом слое на расстоянии г от ядра независимо от направления. [4]
 |
Простейшие волновые функции для водородоподобных атомов. [5] |
Величина ф 2 равна плотности вероятности нахождения электрона в данной точке пространства. [6]
 |
Плотность вероятности нахождения электрона в пространстве ( для простоты взят одномерный случай. [7] |
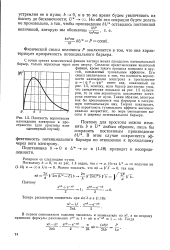
Его смысл заключается в том, что плотность вероятности нахождения электрона в пространстве w - ф 2 W имеет вид, показанный на рис. 1.5, поэтому, если барьер достаточно узок, что схематически показано на рис. 1.5 пунктиром, то за ним вероятность нахождения электрона отлична от нуля. Таким образом, электрон как бы просачивается под барьером в следующую потенциальную яму. Теория показывает, что вероятность туннельного эффекта экспоненциально возрастает, по мере уменьшения высоты и ширины потенциального барьера. [8]
В каких точках в интервале ( 0х /) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова. [9]
Из этой формулы следует, что выражение R nlr2 представляет собой плотность вероятности нахождения электрона на расстоянии г от ядра. На рис. 22.3 приведены графики плотности вероятности для различных состояний водородного атома. На рисунке видно, что наиболее вероятные расстояния электрона от ядра совпадают с радиусами соответствующих боровских орбит. [10]
Из формулы (28.10) следует, что выражение Rni rz представляет собой плотность вероятности нахождения электрона на расстоянии г от ядра. Длинными вертикальными черточками отмечены на графиках радиусы соответствующих боровских орбит. Из рисунка видно, что эти радиусы совпадают с наиболее вероятными расстояниями - электрона от ядра. [11]
Шредиигера - волновое уравнение, являющееся основным уравнением квантовой механики, характеризующим плотность вероятности нахождения электрона в данной единице объема. [12]
Is -, Квадрат этой функции выражает 2s и 2р - орбиталеи водорода плотность вероятности нахождения электрона в пространстве вокруг-ядра. [13]
Если во взаимодействие вступают два различных атома, то максимальная плотность электронного облака ( плотность вероятности нахождения электронов) может сместиться ближе к одному из взаимодействующих атомов, и именно к тому атому, который имеет большее число электронов в валентной оболочке. В предельном случае максимальная плотность электронного облака находится у одного из взаимодействующих атомов, который тем самым превращается в отрицательно заряженный ион, в то время как другой атом превращается в положительный ион. В этом случае связь носит название ионной, поскольку ее можно рассматривать как результат кулоновского притяжения разноименных ионов. [14]
Физическая интерпретация волновой функции заключается в том, что квадрат ее модуля ф 2 представляет плотность вероятности нахождения электрона. Эта величина также имеет симметрию - функций: электронное облако s - функции представляет шаровой слой, а три электронных облака Pxi-Py - и Р - ФУНКЦИЙ сохраняют вытянутость вдоль осей х, г /, z и взаимную ортогональную ориентировку. [15]
Страницы: 1 2 3