Плотность - вероятность - нахождение - электрон
Cтраница 2
Что представляют собой величины г э с точки зрения обычной наглядно-сти - непонятно; неизвестно также, почему именно корень квадратный из плотности вероятности нахождения электрона в данном элементарном объеме dv дает значение волновой функции T J или так называемой условно амплитуды вероятности. Тем не менее, постулат о фундаментальном значении как т з, так и if2 для всей микромеханики, а значит и для химии остается краеугольным камнем: микромеханику называют не только квантовой, но и волновой. [16]
В 1926 г. Борн предположил, что функция W должна быть связана с некоторым физически наблюдаемым свойством электрона через функцию Т2 ( в более общем случае через Y 1.1), если ЧГ - комплексная функция), которая интерпретируется как плотность вероятности нахождения электрона в некоторой точке пространства. Борновская трактовка лучше, поскольку, как видно из дальнейшего, уравнения квантовой механики основаны на представлении об электроне, как о точечном заряде, а не зарядовом облаке. Однако, измеряя среднюю по времени электронную плотность в атоме или молекуле, невозможно различить эти две интерпретации Ч72; поэтому часто бывает удобно и физически наглядно представлять себе Ч72 как плотность электронного облака. [17]
Более точным будет следующее утверждение: вероятность обнаружения электрона в некотором малом объеме ДУ выражается произведением ф2 AV. Таким образом, сама величина ф2 выражает плотность вероятности нахождения электрона в соответствующей области пространства. [18]
Справедливость такого описания подтверждается результатами точных расчетов. Каждая кривая представляет собой линию, вдоль которой плотность вероятности нахождения электронов постоянна. На этих графиках для отдельных МО даны пространственные контуры плотностей, отличающиеся друг от друга последовательно в четыре раза. Диаграммы для Iff и Iff показывают, что более 90 % плотности вероятности заключено в пределах линии, соответствующей плотности 0 053 е - / А3, с радиусом 0 7 А. Для 2ст - орбитали линия той же плотности проходит между ядрами. Полученная из расчета кривая показывает, что 2сг - орбиталь стягивает электроны в область между ядрами так, что по направлению к периферии молекулы плотность распределения спадает значительно медленнее. Эта орбиталь приводит к распределению вероятности нахождения электрона и в области между ядрами, и вокруг обоих ядер лития, отстоящих друг от друга на равновесное расстояние 2 68 А. [19]
Если Y - функция, содержащая чисто мнимое число i - У - 1, то Т, комплексно сопряженная с Y, получается заменой i на - i в Y. Таким образом, 1F 4f - вещественная, повсюду неотрицательная функция, которая физически интерпретируется как плотность вероятности нахождения электрона в точке пространства. [20]
Нельзя предсказать, в какую именно точку пластинки попадет какой-нибудь определенный электрон. Вместо определенных траекторий движения электрона, фигурировавших в теории Бора, волновое уравнение Шредингера характеризует распределение плотности вероятности нахождения электрона в различных точках пространства в атоме или молекуле. Рассматривая различие этой вероятности для разных точек, часто говорят о различной плотности электронного облака, или о различной электронной плотности. Атомной орбиталью мы будем называть волновую функцию, описывающую состояние данного, электрона в атоме и распределение плотности вероятности нахождения электрона в различных точках электронного облака. Впрочем, иногда условно орбиталью называют и соответствующее уравнение и даже само электронное облако, говоря о форме и размерах орбитали. [21]
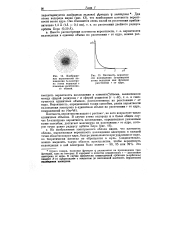 |
Изображение вероятности нахождения ls - электро-на атома водорода с помощью электронного облака.| Плотность вероятности нахождения ls - электрона атома водорода как функция расстояния г от ядра. [22] |
Строго говоря, волновая функция г разлагается на произведение трех функций, одна из которых R содержит в качестве неизвестного г - расстояние электрона от ядра. В случав сферически симметричной орбитали ( s - орбиталь) квадрат R ( г) представляет с точностью до постоянной плотность вероятности нахождения электрона. [23]
Использование этой функции означает, что рассматривается не просто два электрона исходных атомов, а пара электронов, связанных между собой. Для возможности образования такой пары электроны должны обладать антипараллельными спинами, что отвечает выполнению принципа Паули. Только при этом условии происходит перекрывание облаков и плотность вероятности нахождения электронов в пространстве между ядрами атомов выше, чем вне его. На рис. 10 представлена контурная диаграмма этой плотности вероятности для молекулы водорода при антипараллельных спинах электронов и на рис. 11 для аналогичной системы из двух атомов водорода при параллельных спинах электронов. [24]
Состояние электрона описывается одноэлектронной волновой функцией фг, характеризуемой определенным набором квантовых чисел. В отличие от одноцентровой атомной орбитали ( АО) молекулярная орбит аль в общем случае многоцентровая, так как число ядер в молекуле не менее двух. Как и для электрона в атоме, квадрат волновой функции ] г 2 определяет плотность вероятности нахождения электрона или плотность электронного облака. [25]
Состояние электрона описывается одноэлектронной волновой функцией lft, характеризуемой определенным набором квантовых чисел. В отличие от одноцентровой атомной орбитали ( АО) молекулярная ор-биталь в общем случае многоцентровая, так как число ядер в молекуле не менее двух. Как и для электрона в атоме, квадрат волновой функции ф; 2 определяет плотность вероятности нахождения электрона или плотность электронного облака. [26]
Нельзя предсказать, в какую именно точку пластинки попадет какой-нибудь определенный электрон. Вместо определенных траекторий движения электрона, фигурировавших в теории Бора, волновое уравнение Шредингера характеризует распределение плотности вероятности нахождения электрона в различных точках пространства в атоме или молекуле. Рассматривая различие этой вероятности для разных точек, часто говорят о различной плотности электронного облака, или о различной электронной плотности. Атомной орбиталью мы будем называть волновую функцию, описывающую состояние данного, электрона в атоме и распределение плотности вероятности нахождения электрона в различных точках электронного облака. Впрочем, иногда условно орбиталью называют и соответствующее уравнение и даже само электронное облако, говоря о форме и размерах орбитали. [27]
Разрыхляющими называются такие орби-тали, заселение которых способствует диссоциации молекул. Рассмотрим ls - орбитали двух сближающихся атомов водорода и предположим, что эти волновые функции имеют противоположные знаки. При сближении атомов область положительных амплитуд одной орбитали вторгается в область отрицательных амплитуд другой. В соответствии с законами волновой механики интерференция волновых функций приводит к уменьшению результирующей амплитуды в области перекрывания. Поскольку квадрат амплитуды волновой функции определяет плотность вероятности нахождения электронов, это уменьшение касается и ее. [28]
Можно сказать несколько слов и о природе самих электронных возбуждений. Мы уже отметили, что на спектры поглощения ионных кристаллов существенным образом влияет связь электрона с дыркой. Имеются и другие типичные для ионных кристаллов отклонения от формы спектров, обусловленной только зонной структурой, тогда как в ковалентных кристаллах такие эффекты не играют роли. Первый из этих эффектов состоит в деформации кристаллической решетки электроном, находящимся в зоне проводимости. Электроны в зоне проводимости во многих отношениях ведут себя как свободные электроны, хотя плотность вероятности нахождения электрона вблизи металлического иона несколько больше, чем у неметаллического иона. [29]
А различия в значениях квантового числа т; при одних и тех же пи / обозначены нижними индексами справа от букв. Для графического представления атомных орбиталей ( зависимость Ф от г, в и р) требуется четырехмерное пространство, что практически невозможно. Вероятность нахождения электрона на различных расстояниях от ядра можно наглядно выразить при помощи так называемого графика радиального распределения. На рис. 13 приведено радиальное распределение величины 4тг2 [ ЛП) ( г) ] 2, которая характеризует плотность вероятности нахождения электрона на различных расстояниях от ядра. [30]
Страницы: 1 2 3