Плотность - квантовое состояние
Cтраница 1
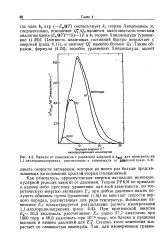 |
Вклады от комплексов с различной энергией в koa для изомеризации 1 1-дихлорциклопропана, рассчитанные в зависимости от давлений ( разд.. [1] |
Плотность квантовых состояний быстро возрастает с энергией ( разд. [2]
 |
Энергетические зоны и межзонные переходы ( гл. V-III для простого полупроводника при Н 0 ( а и Я. 0 ( б. [3] |
Теперь определим плотность квантовых состояний электрона ( дырки) в магнитном поле. [4]
Начнем с плотностей квантовых состояний 8i ( S) и gz () Напомним, как в квантовой статистике определяется плотность квантовых состояний. Проще всего воспользоваться методом Дебая: в кубе с ребром L находим число устойчивых систем стоячих волн длиной Я. Получается некоторая величина, зависящая, естественно, от L и Я. [5]
Начнем с плотностей квантовых состояний Si ( S) и 8г () Напомним, как в квантовой статистике определяется плотность квантовых состояний. Проще всего воспользоваться методом Дебая: в кубе с ребром L находим число устойчивых систем стоячих волн длиной К. [6]
Использование непрерывного распределения допустимо при больших энергиях, когда плотность квантовых состояний велика ( разд. [7]
 |
Векторная диаграмма скоростей частиц, участвующих в ядерной реакции, в лабораторной системе координат и в системе центра масс. [8] |
Относительный импульс двух сталкивающихся частиц р удобно использовать при вычислении плотности трансляционных квантовых состояний в реагирующей системе ( см. примечание на стр. [9]
При таких условиях может оказаться полезным сформулировать результаты в терминах N ( E) - плотности квантовых состояний, или числа квантовых состояний на единицу интервала энергии при энергии Е, что равно производной IP ( EV) no E. [10]
Таким образом, вблизи дна зоны проводимости или около потолка валентной зоны мы можем записать плотность квантовых состояний в энергетическом представлении, щ оно может оказаться бессодержательным, если мы не располагаем экспериментальными данными о значении входящей в него эффективной массы. [11]
Таким образом, вблизи дна зоны проводимости или около потолка валентной зоны мы можем записать плотность квантовых состояний в энергетическом представлении, по оно может оказаться бессодержательным, если мы не располагаем экспериментальными данными о значении входящей в него Эффективной массы. [12]
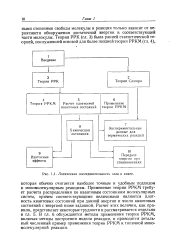 |
Логическая последовательность глав в книге. [13] |
Применение теории РРКМ требует расчета распределения по квантовым состояниям молекулярных систем, причем соответствующими величинами являются плотность квантовых состояний при данной энергии и число квантовых состояний с энергией ниже заданной. Расчет этих величин, как правило, представляет некоторые трудности и рассматривается отдельно в гл. РРКМ, включая методы построения модели реакции, и приводится детальный численный пример применения теории РРКМ к типичной мономолекулярной реакции. [14]
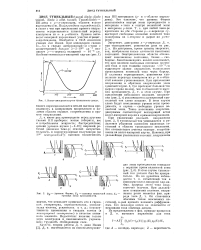 |
Вольт-амперная хар-ка туннельного диода. [15] |
Страницы: 1 2