Плотность - поверхностный ток
Cтраница 3
Поверхностью интегрирования в этом соотношении служит поверхность магнита. Плотность поверхностных токов равна - я X Ж, где п - единичный вектор, нормальный поверхности магнита. Из зтого соотношения с помощью формулы (7.37) легко получить выражение для поля магнитной индукции. [31]
Поверхностью интегрирования в этом соотношении служит поверхность магнита. Плотность поверхностных токов равна - п X М, где п - единичный вектор, нормальный поверхности магнита. Из этого соотношения с помощью формулы (7.37) легко получить выражение для поля магнитной индукции. [32]
Таким образом, имеется скачок тангенциальных составляющих магнитного поля у границы. Величина скачка определяет плотность поверхностного тока в направлении оси волновода. [33]
Той же величиной 8 определяется и глубина проникновения переменного поля в толщу металла. В частности, плотность поверхностного тока i однозначно определяется в этом приближении тангенциальными слагающими магнитного поля Н у внешней поверхности проводника, ибо поле внутри проводника при 8 0 равно нулю, и пограничное условие ( Г) ( § 91, стр. [34]
Той же величиной б определяется и глубина проникновения переменного поля в толщу металла. В частности, плотность поверхностного тока i однозначно определяется в этом приближении тангенциальными слагающими магнитного поля Н у внешней поверхности проводника, ибо поле внутри проводника при 6 0 ровно нулю, и пограничное условие ( I) ( § 91, стр. [35]
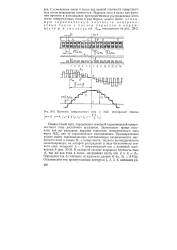 |
Плотность поверхностного тока и МДС многофазной обмотки. [36] |
Однако такой путь определения основной гармонической поверхностного тока достаточно трудоемок. Значительно проще получить тот же результат, выразив плотность поверхностного тока через МДС или ее гармонические составляющие. [37]
 |
Плотность поверхностного тока и МДС многофазной обмотки 3, 7 4, д / 2 / а. 1В с - - - / а. [38] |
Однако такой путь определения основной гармонической поверхностного тока достаточно трудоемок. Значительно проще получить тот же результат, выразив плотность поверхностного тока через МДС или ее гармонические составляющие. В полярной системе координат плотность тока А, так же как токи в пазах, направлена вдоль оси Z и А - Az. [39]
 |
Плотность поверхностного тока 3, 9 4, А2. [40] |
Однако такой путь определения основной гармонической поверхностного тока достаточно трудоемок. Значительно проще получить тот же результат, выразив плотность поверхностного тока через МДС или ее гармонические составляющие. [41]
 |
Характеристики электромагнитного поля. [42] |
Здесь индексами 1 и 2 отмечены среды по обе стороны от границы, а индексы п и т обозначают нормальные и касательные компоненты векторов. Соотношения (1.95) записаны для распространенного случая, когда равны нулю плотность поверхностного тока и плотность поверхностного электрического заряда на поверхности раздела. [43]
 |
Основная гармоническая плотности поверхностного тока ( в однопери-одной модели. [44] |
Таким образом, мы приходим к заключению, что основная гармоническая линейной плотности поверхностного тока представляет собой вращающуюся волну с периодом 2т и амплитудой А1т, перемещающуюся с той же угловой скоростью Q ( или электрической угловой скоростью со в модели), что и основная гармоническая МДС. Независимо от направления, в котором вращается МДС, волна плотности поверхностного тока всегда повернута относительно волны МДС на электрический угол л / 2 или смещена на т / 2 против часовой стрелки. [45]
Страницы: 1 2 3 4