Плотность - число - частица
Cтраница 2
Комптона-Геттинга (8.15), выраженный через плотность N числа частиц на единичный интервал энергии во вращающейся системе. [16]
 |
Плотность распределения вероятности параметра порядка P ( s для различных плотностей.| Зависимость фактора сжимаемости от плотности в системе жестких тонких стержней конечной длины. [17] |
То, что система нитей при плотности числа частиц больше критического значения приближается по своим свойствам к идеальному газу, позволяет ожидать, что при ограничении движения центров масс частиц в этих условиях основной вклад в поверхностные силы будут давать ориентационные эффекты. Ниже приведены результаты расчета для модели прослойки, в которой движение центров масс нитей ограничивалось параллельными линиями на расстоянии Я друг от друга независимо от их ориентации. Ориентационная упорядоченность системы характеризуется величиной s2, которая отражает также характер флуктуации параметра порядка. [18]
Левая часть полученного выражения дает изменение плотности числа частиц в точке х в момент времени t за единицу времени. Поэтому уравнение (84.6) носит название уравнения кинетического баланса. [19]
С - тепловая скорость и п - плотность числа частиц. [20]
Плазма в начальном состоянии считается однородной с плотностью числа частиц N 2 6 - 1015 см-3, что соответствует начальному давлению Рг 50 мТор при комнатной температуре. [21]
АЗ введены па, Т иг 0 - плотность числа частиц, температура и средняя скорость; у. [22]
Для твердых тел нет закона Авогадро, и плотность числа частиц не одинакова в разных веществах. [23]
АЗ введены па, Т иг 0 - плотность числа частиц, температура и средняя скорость; у. [24]
Первое из указанных соотношений означает убывание со временем плотности числа частиц в коагулирующей системе, а второе - сохранение с течением времени общей массы частиц в единице объема системы. [25]
В этом представлении очевидна связь матрицы плотности с плотностью числа частиц. [26]
Если расстояние между частицами значительно меньше Я и если плотность числа частиц одинакова во всех точках объема среды, то расчет по молекулярной теории приводит к тем же выводам, что и феноменологич. Именно, в среде вторичные волны гасят падающую волну и создают преломленную; вне среды интерференция вторичных волн приводит к образованию отраженной волны с фронелевской амплитудой. Если расстояние между частицами сравнимо с X ( практически это имеет место в рентгеновской области), то феноменологич. Тепловое движение молекул обусловливает нарушение условия постоянства плотности частиц и приводит к новому явлению - молекулярному рассеянию света. [27]
В случае бесконечного пространства имеет смысл говорить только о плотности числа частиц. [28]
Постоянные А, В и 0 определяются - через плотность числа частиц п, макроскопическую скорость и и температуру Т, которые выражаются с помощью функции распределения. Чтобы отметить, что эти макроскопические переменные вычисляются для равновесного состояния, им также приписывается индекс нуль. [29]
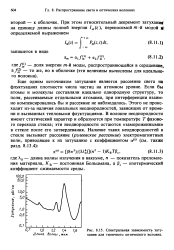 |
Спектральная зависимость затухания для типичного оптического волокна. [30] |
Страницы: 1 2 3 4