Плотность - энергия - разрушение
Cтраница 1
Плотность энергии разрушения, рассмотренная выше, получена из условия равномерного процесса подрастания трещины в цикле нагружения. [1]
 |
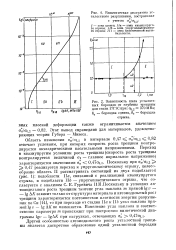
Зависимость 6 от р для наклонной трещины в пластине при растяжении в условиях плоской деформации 26 ]. [2] |
При монотонном нагружении, когда локальна плотность энергии разрушения ( dW / dV) достигает максимального значения ( dW / dV) % R ( dW / dV) c, трещина страгивается. [3]
Выполним оценку этого отличия путем отнесения плотности энергии разрушения к меньшему объему материала. [4]
Необходимо отметить, что для упругопластического разрушения плотность энергии разрушения не служит постоянной материала, так как длина d пластической зоны зависит от критического напряжения. [5]
Один и тот же кинетический процесс, характеризуемый определенной величиной плотности энергии разрушения по уравнению (4.26) или ( что то же) одним и тем же управляющим параметром, определяемым по уравнению (4.20), может быть реализован при многообразии условий внешнего воздействия - при различных параметрах цикла нагружения. [6]
R-кривой можно получить докритпческую диаграмму разрушения или, наоборот, как по известной пз опыта диаграмме разрушения получить плотность энергии разрушения в функции прироста длины трещины. [7]
 |
Трещины на поверхности усохшей земли в виде звездочек с углом 120 в точке образования трещин. [8] |
Абсолютный размер стороны ячейки шестиугольника ориентировочно можно оценить, если принять согласно Гриффитсу, что l4Ey / ns2k, где Е - модуль упругости; у - плотность энергии разрушения; s - напряжение в материале, при котором происходит хрупкое разрушение. [9]
Поскольку в условиях автомодельного роста трещины тангенс угла наклона т прямой lg v - - lg ДЖ зависит только от структуры материала и автомодельный рост трещины характеризуется постоянством плотности энергии разрушения по Си [14], то при переходе от стадии Па к 116 угол наклона прямой lg у - lg A / iT не изменяется. [11]
 |
Трещины на поверхности усохшей земли в виде звездочек с углом. [12] |
Абсолютный размер стороны ячейки шестиугольника ориентировочно можно оценить, если принять согласно Гриффитсу, что l - 4Ey / ns2k) где Е - модуль упругости; у - плотность энергии разрушения; & ъ - напряжение в материале, при котором происходит хрупкое разрушение. [13]
Эта энергия разрушения отличается от энергии разрушения упругого тела тем, что здесь 5Г целиком определяется затратой энергии на работу пластической деформации, Для идеально упругого хрупкого тела по определению d 0 и величина 8Г есть часть внутренней энергии, причем плотность энергии разрушения постоянна. [14]
Эта энергия разрушения отличается от энергии разрушения упругого тела тем, что здесь 5Г целиком определяется затратой энергии на работу пластической деформации, Для идеально упругого хрупкого тела по определению d 0 и величина 5Г есть часть внутренней энергии, причем плотность энергии разрушения постоянна. [15]
Страницы: 1 2