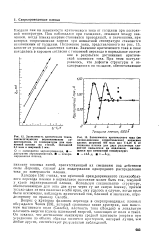
Средняя плотность - энергия
Cтраница 1
Средняя плотность энергии в интервале частот от v до v - - d получится умно / копнем w на dv п па плотность состояний pc / Q 2v2a Q / t3, где ilil элемент телесного угла, в к-ром распространяются фотоны. [1]
Однако средние плотности энергий аддитивны, так как члены, описывающие взаимодействие, в среднем обращаются в нуль. Правда, может понадобиться несколько изменить определение среднего. [2]
Итак, средняя плотность энергии в бегущей звуковой волне пропорциональна плотности среды, квадрату амплитуды и квадрату частоты колебаний. [3]
Таким образом, средняя плотность энергии в помещении прямо пропорциональна мощности источника Р и обратно пропорциональна полному поглощению в помещении. [4]
В стационарных условиях средняя плотность энергии поля в каждой точке пространства не меняется со временем. [5]
Ед показывает отноптение средней плотности энергии к плотности энергии во фронте ударной волны. [6]
Отсюда видно, что средняя плотность энергии пропорциональна плотности среды, квадрату амплитуды волны и квадрату частоты. Подобная зависимость имеет место не только для плоской волны, но и для других видов синусоидальных волн. [7]
Любое наблюдение показывает, что средняя плотность энергии в пространстве по сравнению с этими чудовищными величинами пренебрежимо мала. Эта неестественная энергия должна поэтому как-то компенсироваться. [8]
В качестве основной переменной принимается средняя плотность энергии резонансных колебаний, частоты которых попадают в рассматриваемую полосу. В пределах этсл частотной полосы усредняются параметры, определяющие энергетический баланс в системе. [9]
Следовательно, существует качественная корреляция средней плотности энергии и эрозионной активности ка-витационной области от гидростатического давления. [10]
Он показал, что достижение максимума средней плотности энергии при усреднении по объему образца является критерием, который лучше, чем любые другие, соответствует результатам наблюдений. [12]
Предполагается, что параметры по определению средней плотности энергии выбираются в зависимости от условий работы оптической системы. [13]
Отметим, что при записи выражения средней плотности энергии (5.9) использовано то обстоятельство, что для гармонических волн полная плотность энергии как сумма плотности кинетической и потенциальной энергии равна удвоенной величине кинетической энергии. [14]
В случае черной облучаемой поверхности оно равно средней плотности энергии в падающей волне, в случае зеркально отражающей поверхности оно должно быть в два раза больше, поскольку отраженная волна уносит тот же по абсолютной величине импульс, но противоположного знака. Эту ситуацию мы рассмотрим подробнее, не ограничиваясь случаем нормального падения. [15]
Страницы: 1 2 3