Спектральная плотность - ошибка
Cтраница 1
Спектральная плотность ошибки - сумма двух составляющих дробно-рационального вида, поэтому величину дисперсии ошибки можно вычислить, используя таблицы Мак-Ленна или матрично. [1]
Как видно, спектральная плотность ошибки состоит из двух компонент. Первая соответствует входному сигналу, вторая - помехе. [2]
 |
Составной спектр, полученный сложением спектра полезного сигнала со спектром нежелательного шума. [3] |
Выходная спектральная плотность или спектральная плотность ошибки сложной цепи может быть записана сразу. [4]
Аналогично можно получить функции спектральных плотностей ошибки при остальных сочетаниях воздействий. [5]
Таким образом, функция спектральной плотности ошибки регулирования при одном воздействии типа п равна произведению функции спектральной плотности воздействия на квадрат амплитудной частотной характеристики системы по величине е регулируемого процесса. [6]
Чтобы обеспечить минимум интеграла от спектральной плотности ошибки, достаточно обеспечить минимум его приращения на каждой полосе. [7]
Покажем, как может быть найдена спектральная плотность ошибки S9 ( ю) для случая, когда на вход системы поступает только полезный сигнал ( задающее воздействие), и для случая, когда система находится под влиянием двух стационарных случайных воздействий: задающего a ( t) и возмущающего n ( t) ( помехи), приложенных как к различным точкам системы, так и к одной из них. [8]
Из рассмотрения ее может быть далее найдена спектральная плотность ошибки. [10]
 |
Графический мет Д определения средне-квадратическои ошибки. [11] |
Выше было показано, каким образом может быть найдена спектральная плотность ошибки динамической системы, находящейся в общем случае под влиянием задающего и возмущающего воздействия ( см. выражение (8.53)), а также была получена формула (8.55), с помощью которой можно вычислить дисперсию ошибки. Рассмотрим графический и аналитический методы. [12]
 |
Метод адаптации с балансом энергии.| Метод адаптации с высоким коэффициентом усиления. [13] |
Рассмотрен универсальный метод адаптации, который основан на минимизации моментов спектральной плотности ошибки системы управления с обратной связью. Универсальный метод адаптации устанавливает связь между различными, с первого взгляда не связанными методами адаптации, которые были описаны ранее в технической литературе. Например, при введении соответствующих упрощений из общего метода можно легко получить такие методы адаптации, как адаптацию с опорной моделью, адаптацию с балансом энергии и адаптацию с высоким коэффициентом усиления. Полученный метод адаптации обеспечивает основу для новых адаптивных методов, которые можно получить, вводя подходящие для каждого частного случая упрощения. [14]
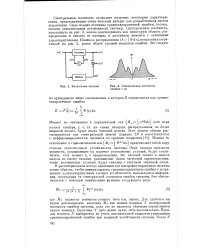 |
Блок-схема системы.| Спектральная плотность ошибки е ( t. [15] |
Страницы: 1 2 3
