Спектральная плотность - помеха
Cтраница 2
При различных значениях т и а функция (4.11.23) может быть использована для аппроксимации широкого класса спектральных плотностей помехи. [16]
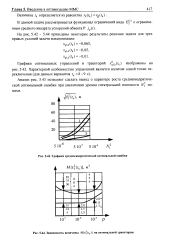 |
Зависимость величины Af [ ef ( / t ] на оптимальной траектории. [17] |
Анализ рис. 5.43 позволяет сделать вывод о характере роста среднеквадратиче-ской оптимальной ошибки при увеличении уровня спектральной плотности N помехи. [18]
Поэтому, строго говоря, факт потери устойчивости под действием помех можно считать действительным, только если спектральная плотность помехи существенно отлична от нуля при частотах выше ю0 14 1 / сек. [19]
Искомая спектральная плотность сигнала 5 ( /) должна быть такой, чтобы, будучи добавленной к спектральной плотности помехи N ( /), она обеспечила постоянство этой суммы и независимость ее от частоты. [20]
Из (6.57) следует, что минимальная вероятность ошибки при оптимальном когерентном приеме определяется энергией разности сигналов и спектральной плотностью помехи. [21]
Анализ (6.58) показывает, что минимальная вероятность ошибки падает с ростом расстояния между сигналами и длительности сигналов и растет, если увеличивается спектральная плотность помехи. [22]
Анализ (6.58) показывает, что минимальная вероятность ошибки падает с ростом расстояния между сигналами и длительности сигналов и растет, если увеличивается спектральная плотность помехи. [23]
Этот случай представлен на рис. 8.2, где 8х ( ш) - спектральная плотность сигнала и Se ( u) - спектральная плотность помехи. [24]
Этот случай представлен на рис. 8.2, где Sx ( со) - спектральная плотность сигнала и S ( со) - спектральная плотность помехи. [25]
Анализируя (6.76), (6.77), (6.85) и (6.86), можно заметить, что для определения помехоустойчивости некогерентного приемника необходимо знать только энергию сигналов и спектральную плотность помехи. Сигнал оставляет свои следы в виде деформации распределения Релея в обобщенное распределение Релея. [26]
Анализируя (6.76), (6.77), (6.85) и (6.86), можно заметить, что для определения помехоустойчивости некогерентного приемника необходимо знать только энергию сигналов и спектральную плотность помехи. Сигнал оставляет свои следы в виде деформации распределения Релея в обобщенное его распределение. [27]
Оптимальный когерентный прием дискретных сигналов на фоне помех целесообразен, когда форма и параметры передаваемых сигналов известны на приемной стороне абсолютно точно, искажения сигналов в гауссовом канале с постоянными параметрами отсутствуют, спектральная плотность помех известна, синхронизация принимаемых и опорных сигналов идеальная, аппаратурные погрешности отсутствуют. Оптимальный алгоритм когерентного приема сигналов (6.37) на фоне помех позволяет определить в гильбертовом пространстве сигналов расстояние между принятым сигналом и всеми передаваемыми сигналами и выбрать тот, к которому принятый ближе всего. Оптимальный приемник, работающий по этому алгоритму, обладает потенциальной помехоустойчивостью. [28]
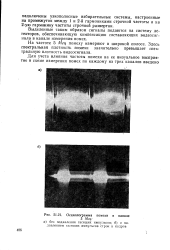 |
Осциллограмма помехи в канале. [29] |
На частоте 5 Мгц помеху измеряют в широкой полосе. Здесь спектральная плотность помехи значительно превышает спектральную плотность видеосигнала. [30]
Страницы: 1 2 3