Взаимно перпендикулярная площадка
Cтраница 3
Следовательно, касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по знаку. Это свойство обычно называют законом парности касательных напряжений, причем оно имеет место во всех случаях, когда имеются касательные напряжения. [31]
Следовательно, касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по знаку. Это свойство обычно называют законом парности касательных напряжений, причем оно имеет место во всех случаях, когда имеются касательные напряжения. [32]
Другими словами, касательные напряжения на взаимно перпендикулярных площадках равны друг другу. [33]
Из рисунка видно, что на взаимно перпендикулярных площадках касательные напряжения равны по величине и противоположны по знаку. Это свойство называется законом парности касательных напряжений. [34]
Через каждую точку тела можно провести три взаимно перпендикулярные площадки, в которых касательные напряжения равны нулю. Эти площадки называют главными, а действующие в них нормальные напряжения - главными напряжениями. [35]
Через каждую площадку тела можно провести три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю. Эти площадки называются главными площадками в рассматриваемой точке, а направление нормалей к ним - главными направлениями. Действующие на главных площадках нормальные напряжения называются главными напряжениями и обозначаются через uj, с. Нормальные напряжения в данной точке достигают на главных площадках экстремальных значений. [36]
Через каждую точку тела можно провести три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю. Эти площадки называются главными площадками в рассматриваемой точке, а направления нормалей к ним - главными направлениями. [37]
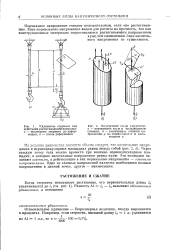 |
Внутренние силы упругости. а - внутренние силы в произвольном сечении. б - разложение полного напряжения р на нормалыюе а и касательное т. [38] |
Через каждую точку тела можно провести три взаимно перпендикулярные площадки, в которых касательные напряжения равны нулю. Эти площадки называют главными, а действующие в них нормальные напряжения - главными напряжениями. Одно из главных напряжений является наибольшим полным напряжением в данной точке, другое - наименьщим. [39]
Через каждую площадку тела можно провести три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю. Эти площадки называются главными площадками в рассматриваемой точке, а направление нормалей к ним - главными направлениями. Действующие на главных площадках нормальные напряжения называются главными напряжениями и обозначаются через jlf ( 72 и из. Нормальные напряжения в данной точке достигают на главных площадках экстремальных значений. [40]
Иными словами, касательные напряжения по двум взаимно перпендикулярным площадкам, направленные перпендикулярно к линии пересечений этих площадок, равны по величине и об-ратны по знаку. Эта теорема известна под названием закона парности касательных напряжений. Так как по площадкам ABGE и OCDF напряжения тгу и ixy равны нулю, то на основании закона парности касательных напряжений равны нулю и напряжения Tyz по площадкам AOFE и BCDG и туж по площадкам АВСО и EGDF, что и подтверждает сказанное в примечании внизу на этой странице. [41]
Если известны напряжения, действующие по двум взаимно перпендикулярным площадкам, проходящим через данную точку, то определение напряжений по любым другим площадкам, а также положений главных площадок и площадок сдвига можно проводить графическим способом - с помощью так называемого круга Мора. [42]
Если известны напряжения, действующие по двум взаимно перпендикулярным площадкам, проходящим через данную точку, то определение напряжений по любым другим площадкам, а также положений главных площадок и площадок сдвига можно проводить графическим способом-с помощью так называемого круга Мора. [43]
Вследствие этих равенств, напряжения по трем взаимно перпендикулярным площадкам, проходящим через некоторую точку в жидкости, характеризуются не девятью, как указывалось выше, а шестью величинами. Можно доказать, что эти же шесть величин определяют напряжение поверхностной силы по любой другой площадке, проходящей через ту же точку. Таким образом, напряженное состояние жидкости в любой точке характеризуется шестью величинами: тремя нормальными напряжениями и тремя касательными по трем взаимно перпендикулярным площадкам, проходящим через эту точку. [44]
Тензор характеризует сразу три напряжения по трем взаимно перпендикулярным площадкам и используется для описания физических явлений и процессов, происходящих в упругой среде. В механике сплошной среды используется трехмерное евклидово пространство с различными системами координат. Примененный для описания напряженного состояния точки тензор напряжений инвариантен относительно преобразования прямоугольных координатных осей. Тензор напряжений симметричный, так как коэффициенты матрицы симметричны относительно главной диагонали и равны между собой. Задать тензор напряжений - значит определить напряженное состояние в данной точке тела. В частных случаях напряженное состояние точки определяет напряженное состояние всего тела ( при простом растяжении - сжатии), такое напряженное состояние называется однородным. [45]
Страницы: 1 2 3 4