Поверхность - постоянная фаза
Cтраница 3
Поэтому такая волна и называется плоской. Поверхность постоянной фазы перемещается в направлении k со скоростью ш / k v, где v ш / 2тг - линейная частота. В заданной плоскости, определяемой некоторым постоянным значением kr, физическая величина ( А или /) осциллирует с частотой и. [31]
Электромагнитное поле в первой среде в том месте, где происходит наложение падающей и отраженной волн ( область внутри треугольника на рис. 3.12), тоже образует неоднородную плоскую волну, распространяющуюся параллельно границе раздела. Поверхности постоянной фазы этой волны, как и неоднородной волны во второй среде, представляют собой плоскости, перпендикулярные границе раздела. Амплитуда этой волны зависит от z, изменяясь периодически с пространственным периодом A / coscp ( A, - длина падающей волны в первой среде), в отличие от экспоненциального затухания вдоль z амплитуды неоднородной волны во второй среде. [32]
Полученное нами уравнение известно в геометрической оптике как уравнение эйконала. Определяемые им поверхности L const являются поверхностями постоянной фазы и, следовательно, определяют фронт волны. [33]
Измерения радиационной силы может использоваться для калибровки гидрофонов по следующей процедуре. Сначала определяют общую мощность, проходящую через поверхность постоянной фазы в поле гармонического акустического источника. [34]
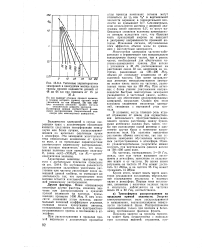 |
Типичные характеристики замираний в наихудшем месяце вдоль трассы прямой видимости длиной от 48 до 64 км при просвете от 15 до 30 м. [35] |
Энергия электромагнитных волн распространяется в направлении, перпендикулярном поверхности постоянной фазы. Распространение-прямолинейно только при плоском и бесконечно протяженном фазовом фронте. [36]
Другим примером гладкой системы может служить вогнутая металлическая поверхность, в частности круглый резонатор. Действительно, вдоль окружности этого резонатора может бежать волна, причем поверхность постоянной фазы имеет угловую скорость со / /, где со - частота колебаний в резонаторе, а / - число волн, укладывающихся вдоль окружности. [37]
Из этого выражения следует, что вся объемная структура перемещается вдоль оси z со скоростью, определяемой условием kzcosy - cof const и действительно равной co / & cosp c / cosp. Участки любой плоскости z const, на которых множитель cos ( bcsinp) сохраняет знак, представляют собой поверхности постоянной фазы, называемые эквифазными. Однако целиком плоскости z const эквифазными поверхностями не являются, ибо там, где изменяется знак cos ( kx sin p), общая фаза скачком меняется на тт. Поэтому сплошного волнового фронта в его обычном понимании здесь не существует. Более того, поскольку направления скачков нельзя считать заданными ( ведь фаза известна с точностью до слагаемого, кратного 2тг), в выборе даже ориентировочной формы фронта существует произвол. [38]
 |
Гиперболические каустики, ограничивающие поле гауссова пучка. [39] |
Однако эти сведения не слишком наглядны. Более интересен другой подход, при котором отыскиваются условия постоянства фазы. Такая поверхность называется поверхностью постоянной фазы или волновым фронтом. [40]
Электромагнитная волна называется плоской, если вектор волны имеет одну и ту же величину во всех точках любой плоскости, перпендикулярной направлению распространения волны. От плоскости к плоскости эти векторы, конечно, изменяются. Можно сказать, что поверхностями постоянной фазы в плоской волне являются плоскости, перпендикулярные направлению распространения. Волна называется монохроматической, если векторы волны изменяются со временем по гармоническому закону с определенной одной частотой. [41]
В дальнейшем будут рассмотрены и другие решения. Сферические монохроматические волны, у которых поверхности постоянной фазы представляют собой концентрические сферы, изучаются в § 1.5. В отличие от плоской волны, амплитуда которой всюду одинакова, амплитуда сферической волны обратно пропорциональна расстоянию до центра. [42]
Для получения этих законов на основе электромагнитной теории рассмотрим идеализированный случай бесконечной плоской границы раздела двух неподвижных однородных изотропных сред, каждая из которых занимает целое полупространство. Пусть в одной из этих сред задана приходящая из бесконечности плоская монохроматическая волна. Эта падающая на границу волна, поверхности постоянной фазы которой представляют собой неограниченные плоскости, порождает волновой процесс в обеих средах, который мы собираемся исследовать. [43]
Такое же утверждение верно и для одного источника, движение которого можно разложить на два движения. Поскольку любую функцию времени можно представить в виде интеграла Фурье по гармоническим функциям, то волновое движение линейной среды можно разложить на гармонические волны. Через произвольную точку гармонической волны можно провести единственную поверхность постоянной фазы, которая называется волновой поверхностью, или фронтом волны. [44]
Напряженность поля убывает об - диполя ратно пропорционально первой степени расстояния. Представляемая формулами (61.43) волна называется сферической. Она распространяется в направлении радиус-вектора. Поверхности постоянной фазы этой волны являются сферами. Скорость волны ( фазовая) равна скорости света. [45]
Страницы: 1 2 3 4