Поверхность - энергия
Cтраница 1
Поверхность энергии для действительной химической реакции всегда, по меньшей мере, двухмерна ( обычно - многомерна), так как она должна включать по одному измерению для каждого межядерного расстояния всех ядер, участвующих в реакции. В каждом случае, однако, имеется некоторая начальная конфигурация, для которой собственная функция системы может быть с хорошим приближением представлена в одном измерении при помощи плоской волны, распространяющейся в направлении области пространства конфигураций, которая соединяет начальную область с областью продуктов. Имеется также область, где собственная функция для конфигурации системы, представляющей продукты, может быть с хорошим приближением выражена в одном измерении посредством движущейся плоской волны. Таким образом, всегда будет возможно разложить точную собственную функцию системы так, что она будет представлена, по меньшей мере ассимптотически, плоской волной, которую мы назовем прошедшей волной, распространяющейся от активированного состояния вниз к долине, отвечающей продуктам реакции. Отношение амплитуды прошедшей волны к амплитуде падающей волны определяет коэфициент прохождения. Точно так же отношение амплитуды отраженной волны к амплитуде падающей волны определяет коэфициент отражения. [1]
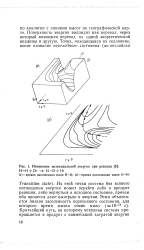 |
Изменение потенциальной энергии при реакции. [2] |
Поверхность энергии выглядит как перевал, через который возможен переход из одной энергетической впадины в другую. [3]
Понятие поверхностей энергии оказалось чрезвычайно полезным для анализа многих поверхностных явлений, особенно явлений роста кристаллов. Если принимать удельную свободную поверхностную энергию как работу, которую необходимо израсходовать, чтобы разорвать связи, то из этого неизбежно следует, что а анизотропна и для различных граней кристалла имеет разную величину. Поэтому значение 0 находится в тесной связи со спайностью кристаллов. [4]
 |
Направления радиуса-вектора и нормали к поверхности энергии.| Связь скорости с величиной эффективной массы и густотой поверхностей энергии. [5] |
Для эллипсоидальных поверхностей энергии радиус-вектор и нормаль не коллинеарны, поэтому направления скорости и квазиимпульса не совпадают. [6]
Необычный характер поверхностей энергии в кремнии и германии заставляет усомниться в возможности применения теоремы Ваннье [4 - 7] без специальной проверки. Нами развит метод, позволяющий определить пределы применимости теоремы Ваннье и оценить поправки, связанные с наличием нескольких минимумов энергии в зоне проводимости и приближенным вырождением изоэнергетических поверхностей в валентной зоне. В принципе этот метод точен и приводит к более глубокому пониманию теоремы Ваннье. Наш подход кажется более удобным в исследуемых здесь вопросах, которые ранее не рассматривались. [7]
Точность теоретических расчетов поверхностей потенциальйой энергии системы атомов недостаточна для вычисления энергии активации Еа. Поэтому приходится прибегать либо к полуэмпирическим методам, либо использовать величины Еа, полученные независимым путем из опыта. [8]
Движение таких систем по поверхности энергии не может быть описано с помощью теоремы Лиувилля, так как последняя соблюдается только при объемном распределении систем. Однако если данная система состоит из большого числа частей, то практически не нарушая условий микроканонического распределения, его можно заменить объемным распределением, удовлетворяющим следующим требованиям. [9]
В области взаимодействия молекул поверхность энергии ( рис. 8) имеет те же свойства, что и поверхность для одной молекулы. [10]
На рис. 15.11 показана поверхность энергии связи для восьмидесяти одного комплекса, рассчитанная на основе выражения (15.16) и дающая наглядное представление о взаимосвязи между комплексами. [11]
Здесь 5 - плотность поверхностей энергии когезии, т.е. энергия югезии, приходящаяся на единицу поверхности. [12]
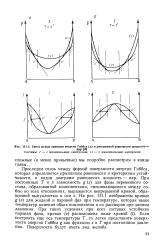 |
Связь между кривыми энергии Гиббса ( а и диаграммой равновесия жидкость-пар ( б. [13] |
Проследим связь между формой поверхности энергии Гиббса, которая определяется принципом равновесия и критериями устойчивости, и видом диаграмм равновесия жидкость - пар. На рис. II 1.1 изображены кривые g ( x) для жидкой и паровой фаз при температуре, которая выше температур кипения обоих компонентов и их растворов при данном давлении. Если построить еще ось температуры Г, то легко представить поверхности энергии Гиббса g как функцию х и Т при постоянном давлении. [14]
Согласно существующей упрощенной теории, рассматривающей поверхности одинаковой энергии в кубической решетке как шаровые, магнитное поле, параллельное току, не должно было бы изменить сопротивления полупроводника с решеткой правильной кубической системы. [15]
Страницы: 1 2 3 4