Срединная поверхность

Cтраница 3

Оболочки, срединная поверхность которых представляет собой поверхность вращения ( фиг. Здесь приводятся расчетные формулы только для симметричных оболочек, находящихся под внутренним или наружным давлением. [31]

Толстостенная труба. [32]

Оболочка, срединная поверхность которой представляет собой поверхность вращения ( рис. 42, а), называется симметричной. Рассмотрим расчет симметричных оболочек, нагруженных давлением, симметричным относительно оси оболочки. [33]

Толстостенная труба. [34]

Оболочка, срединная поверхность которой представляет собой поверхность вращения ( рио. Рассмотрим расчет симметричных оболочек, нагруженных давлением, симметричным относительно оси оболочки. [35]

Если метрика срединной поверхности меняется достаточно медленно по сравнению с w и %, то Я. [36]

Рассмотрим прогиб срединной поверхности, отмеченной на рисунке штриховкой. [37]

Геометрия аппроксимированной срединной поверхности замкнутой оболочки вращения и положительные направления внутренних силовых факторов в сечении z.| Схемы определения геометрических параметров срединной поверхности характерных конусных участков аппроксимированной тонкостенной оболочки. [38]

Указанная аппроксимация срединной поверхности приводит к существенному сокращению объема вычислительных операций и позволяет создать единый алгоритм численного расчета оболочек вращения переменной жесткости со сложной геометрией, в том числе при наличии разрывов в образующей срединной поверхности. При этом толщину и механические характеристики принимают постоянными в окружном направлении: h ( si6i) / z ( s -), Et ( SjOf) E ( SJ), ar ( sr - 0 -) at ( s -); материал оболочки в каждом коническом элементе считают изотропным. [39]

Перемещения точек срединной поверхности условимся разлагать на составляющие и, v и w, которые имеют в каждой точке недеформированной поверхности направления координатных осей ( 0, z / 0, z0) ( рис. 136), построенных так, что ось z0 имеет направление главной нормали, ось у0 направлена по касательной к параллельному кругу в сторону возрастания угла 6, наконец, ось х0 совпадает с образующей цилиндра так, что ( 0, у0, z0) представляет собой право-винтовую систему. [40]

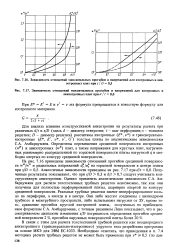Зависимость отношений максимальных прогибов и напряжений для изотропных и анизотропных плит при s / D 0 5.| Зависимость отношений максимальных прогибов и напряжений для изотропных и. [41]

Определены перемещения срединной поверхности изотропных ( WH) и анизотропных ( vva) плит, а также напряжения для круглых плит, нагруженных равномерно распределенной по торцовой поверхности плиты нагрузкой q и свободно опертых по контуру срединной поверхности. [42]

Напряжения в срединной поверхности получаются из этих формул, если отбросить двузначные члены. [43]

Угловая деформация срединной поверхности также принимается равной нулю. Это допущение аналогично допущению, принимаемому в теории стесненного кручения тонкостенных стержней, согласно которому угловая деформация срединной поверхности считается равной нулю, несмотря на наличие касательных напряжений стесненного кручения. [44]

Схема образования оболочки вращения.| Аксонометрия срединной поверхности оболочки вращения. [45]

Страницы: 1 2 3 4