Эквифазная поверхность
Cтраница 3
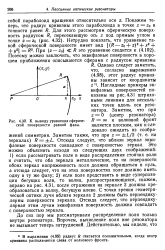 |
К выводу уравнения сферической поверхности равной фазы. [31] |
Наглядные примеры эк-вифазных поверхностей показаны на рис. 4.31 штриховыми линиями для нескольких точек вдоль оси резонатора. Заметим, что при z 0 ( центр резонатора) R оо и волновой фронт является плоским, как и следовало ожидать из соображений симметрии. Отсюда следует, что вблизи зеркал эквифазные поверхности совпадают с поверхностью зеркал. Это можно объяснить исходя из следующих двух соображений: 1) если рассматривать поле в виде распределения стоячих волн и считать, что оба зеркала металлические, то на поверхности обоих зеркал напряженность поля должна обращаться в нуль, а отсюда следует, что на этих поверхностях поле должно иметь одну и ту же фазу; 2) если поле представить в виде суперпозиции бегущих волн, то волна, распространяющаяся, скажем, вправо на рис. 4.31, после отражения на зеркале 2 должна преобразоваться в волну, бегущую влево. С точки зрения геометрической оптики лучи вблизи зеркала 2 должны быть перпендикулярны поверхности зеркала. Отсюда следует, что перпендикулярная этим лучам эквифазная поверхность должна совпадать с поверхностью зеркала. [32]
Пусть активная среда сечения 2а X 2я размещена внутри телескопического резонатора ( рис. 3.11); ее показатель преломления для простоты примем равным единице. Проследим, скажем, за судьбой затравочного излучателя, которое в начальный момент времени испускается вблизи выпуклого зеркала в сторону вогнутого. В качестве отсчетной выберем расположенную у выпуклого зеркала сферическую эквифазную поверхность расходящейся волны, центр кривизны которой находится в общем фокусе зеркал. [33]
Операция ОВФ заключается в придании волне прямо противоположного направления распространения и, с точностью до постоянного множителя, комплексно сопряженного распределения амплитуды. Это означает, что у исходной и обращенной ( сопряженной) волн совпадают эквифазные поверхности и форма распределений интенсивности по сечению. [34]
На рис. 2.28 штриховой дугой, касающейся зеркала, изображена эквифазная поверхность расходящейся волны, движущейся по направлению к этому зеркалу. Эта же поверхность является эквифаз-ной и для сходящейся волны, движущейся уже от зеркала. Поэтому излучение волны, падающее на край зеркала и затем образующее сходящуюся волну, проходит между касающимися зеркала эквифазными поверхностями этих волн суммарное расстояние 2е, которое, как нетрудно убедиться ( подсчитав, исходя из геометрии резонатора, кривизны волн), равно Л экв - Таким образом, при изменении Л э к в на единицу разность фаз между расходящейся и порождаемой ею за счет краевой дифракции сходящейся волнами изменяется на 2тг, что и приводит к квазипериодичности свойств неустойчивых резонаторов. [35]
ЕО-максимальное значение этого поля, а интегрирование производится по объему, занимаемому активной средой. Уместно привести в качестве примера симметричный резонатор, состоящий из двух зеркал, радиусы кривизны которых много больше, чем длина резонатора. Тогда размер пятна моды w будет приблизительно постоянным по всей длине резонатора и равным значению w0 в центре резонатора. Аналогичным образом радиус кривизны эквифазных поверхностей R будет достаточно большим и волновые фронты можно считать плоскими. [36]
Раз поле должно обращаться в нуль, то гауссов пучок нужно использовать в форме стоячей волны, поскольку в стоячей волне имеются узловые поверхности - поверхности, на которых волна обращается в нуль. Идея состоит в том, чтобы одну из таких узловых поверхностей гауссова пучка совместить, скажем, с первым зеркалом резонатора, при этом некоторую другую узловую поверхность совместить со вторым зеркалом резонатора. Эта идея тем более привлекательна, что волновые фронты или эквифазные поверхности гауссова пучка - а узловая поверхность стоячей волны есть частный случай такой поверхности - имеют как раз сферическую форму. [37]
Предположим также, что исходные зеркала 1 и 2 удалены. Теперь резонатор будет образован зеркалами 1 и 2, и распределение поля внутри резонатора, очевидно, не изменится. Таким образом, если заданы радиусы кривизны Ri и R2 зеркал 1 и 2, а также расстояние между ними L, то модовую картину можно получить при условии, что эквифазные поверхности совпадают с поверхностями зеркал в месте их расположения. [38]
Теперь рассмотрим, как действует совокупность множества эквифазных линий объемной голограммы. Освещающая волна, отразившись от элемента одной поверхности, возвращается к другой, проходя расстояние К. Поэтому волны, отраженные соседними эквифазными поверхностями, складываются в фазе. В результате совместного действия множества таких кривых зеркал волна, формирующая мнимое изображение объекта, многократно усиливается. Совокупность множества эквифазных поверхностей выполняет также функции фильтра, отражающего лишь волну определенной длины. [39]
Наглядные примеры эк-вифазных поверхностей показаны на рис. 4.31 штриховыми линиями для нескольких точек вдоль оси резонатора. Заметим, что при z 0 ( центр резонатора) R оо и волновой фронт является плоским, как и следовало ожидать из соображений симметрии. Отсюда следует, что вблизи зеркал эквифазные поверхности совпадают с поверхностью зеркал. Это можно объяснить исходя из следующих двух соображений: 1) если рассматривать поле в виде распределения стоячих волн и считать, что оба зеркала металлические, то на поверхности обоих зеркал напряженность поля должна обращаться в нуль, а отсюда следует, что на этих поверхностях поле должно иметь одну и ту же фазу; 2) если поле представить в виде суперпозиции бегущих волн, то волна, распространяющаяся, скажем, вправо на рис. 4.31, после отражения на зеркале 2 должна преобразоваться в волну, бегущую влево. С точки зрения геометрической оптики лучи вблизи зеркала 2 должны быть перпендикулярны поверхности зеркала. Отсюда следует, что перпендикулярная этим лучам эквифазная поверхность должна совпадать с поверхностью зеркала. [40]
Сначала коснемся расходимости излучения эрмитовых и лагер-ровых пучков с произвольными индексами ( § 1.2), ограничившись тем наиболее важным случаем, когда их параметры р и w действительны. Среди этих пучков тот единственный, который обладает настоящим сферическим волновым фронтом - гауссов, - нами уже рассмотрен. Выражения для распределений комплексной амплитуды остальных пучков, помимо множителя exp [ ( zfr / 2p) ( я i) ], содержат еще и другие влияющие на общую фазу множители, приводящие либо к скачкам фазы на я, либо к медленному ее изменению. Мы и тут будем говорить о геометрической компоненте расходимости ( аг Ь / р) и дифракционной, которая имеет место при р, хотя такое разделение здесь носит более условный характер, чем при подлинной сферической эквифазной поверхности. [42]
Страницы: 1 2 3
