Зеркальный поворот

Cтраница 2

Q и С1 относительно оси вращения третьего порядка, перпендикулярных плоскости молекулы, и двух зеркальных поворотов S1, и SI относительно той же оси третьего порядка. [16]

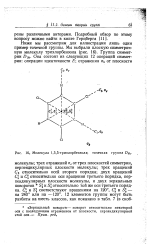Молекула 1 3 5-трихлорбензола. точечная группа D3 /. [17]

С и Сд относительно оси вращения третьего порядка, перпендикулярных плоскости молекулы, и двух зеркальных поворотов S и S относительно той же оси третьего порядка. [18]

Сочетание поворота на некоторый угол jv и отражения в плоскости, перпендикулярной этой оси, называется зеркальным поворотом. [19]

Мы видим, что операция (11.3), равная произведению отражения аг и поворота на угол 0, есть зеркальный поворот, тогда как операция (11.4), равная произведению инверсии и поворота на угол 0, есть инверсионный поворот. [20]

К объяснению метода зеркального наложения. а картина дисперсии в окрестности линии стронция К - 4606 А, б та же картина, испытавшая зеркальный поворот относительно нулевой полосы, в картина зеркального наложения, г картина зеркального наложения при большей плотности.| Принципиальная схема трехлучевого интерферометра. [21]

Она вставляется в половину сечения пучка, чтобы не заслонить вторую его половину, которая не должна испытывать зеркального поворота. [22]

С помощью аналогичных рассуждений можно показать, что произведение taSh ( a) ( a 1 0) является зеркальным поворотом вокруг некоторой точки и что taSk ( 0) есть произведение отражения в некоторой плоскости ofc на трансляцию вдоль этой плоскости. [23]

Несложные геометрические построения показывают [78], что преобразованиями симметрии могут быть отражения в плоскостях, повороты вокруг осей симметрии и зеркальные повороты. [24]

Несложные геометрические построения показывают [69], что преобразованиями симметрии могут быть: а) отражения в плоскостях, б) повороты вокруг осей симметрии, в) зеркальные повороты. [25]

Из ( 6 2) и ( 6 3) следует, что совокупность всех поворотов на один и тот же угол образует класс и что совокупность всех зеркальных поворотов на один и тот же угол также образует класс. [26]

Более светосильное устройство состоит из призмы Дове ( рис. 14.17, 6), Она вставляется в половиву сечения пучка, чтобы не заслонить вторую его половину, которая не должна испытывать зеркального поворота. [27]

Помимо перестановочной есть и другая симметрия: определенные конфигурации тождественных ядер приводят к симметричному потенциальному полю, в котором движутся электроны и которое не меняется при поворотах в пространстве, отражениях в тех или иных плоскостях, зеркальных поворотах, инверсии всего пространства и т.п. Коль скоро потенциальная поверхность вводится в системе координат, начало которой находится в центре масс, то обычно все эти преобразования пространства совершаются так, чтобы центр масс при них не менял своего положения. Это означает, что все элементы симметрии, с помощью которых осуществляются преобразования, оставляют центр масс неизменным. Другими словами, рассматриваются операции, образующие точечные группы симметрии. [28]

Группы симмет - Группа О имеет только оси ( 8С3, 6С2, 6С4г. [29]

В группе S основным элементом является сочетание поворота вокруг оси С с отражением в плоскости ( 0), перпендикулярной этой оси. Зеркальный поворот ведет к появлению и других элементов симметрии. [30]

Страницы: 1 2 3 4