Результирующий поворот

Cтраница 1

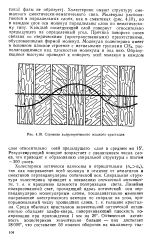Строение холестерического жидкого кристалла. [1]

Результирующий поворот возрастает с увеличением числа слоев, что приводит к образованию спиральной структуры с шагом - 300 слоев. [2]

Результирующий поворот определяется последовательностью трех указанных поворотов, т.е. матрицей А Ах-Аф - Аф. Коль скоро каждая из матриц-сомножителей ортогональна ( в чем нетрудно убедиться прямой проверкой), то ортогональной будет и матрица А. [3]

Полученное представление результирующего поворота вектором говорит о том, что для малых углов операции конечного вращения можно считать коммутативными. Можно считать при этом, что повороты на углы ф, ), 0 совершаются вокруг осей х, у, г. Последнее замечание используется при выборе обобщенных координат для описания малых колебаний упруго закрепленного твердого тела ( см. том I, стр. [4]

Формула (5.10) показывает, что результирующий поворот зависит от порядка, в котором производятся составляющие повороты. [5]

Последняя формула показывает, что результирующий поворот двух конечных поворотов твердого тела вокруг неподвижных осей зависит от порядка выполнения этих поворотов. [6]

Требуется найти угол и эйлерову ось результирующего поворота. [7]

Нетрудно составить также выражение параметров Родрига - Гамильтона результирующего поворота ( обозначим их v0, v1 ( v2, v3) 10 параметрам Х0, Xlt X2, X3 и [ 10, tj, [ i2, [ i3 слагаемых поворотов. [8]

На основании приведенных выражений можно сделать вывод о том, что угол 2ф результирующего поворота исходного кватерниона д, определяемый выражением (1.9.5), зависит от траектории элементарных поворотов и принимает два значения. Одно из них соответствует случаю, когда & о - О) б / о, а другое - когда & о - О) - б / о - При этом оси вращения, задаваемые вектором г для каждой траектории поворотов, разные. [9]

В результате последовательного выполнения двух поворотов, соответствующих кватернионами Ъх и Ьу, получился третий результирующий поворот, соответствующий кватерниону Ьух ЪУЪХ. [10]

В результате последовательного выполнения двух поворотов, соответствующих кватернионами Ъх и Ьу, получился третий результирующий поворот, соответствующий кватерниону Ъух ЪУЪХ. [11]

Можно, разумеется, получить формулу (7.10.2) и элементарным путем, не обращаясь к формуле результирующего поворота. [12]

На основании приведенных выражений можно сделать вывод о том, что угол 2 - 0 результирующего поворота исходного кватерниона д, определяемый выражением (1.9.5), зависит от траектории элементарных поворотов и принимает два значения. Одно из них соответствует случаю, когда & о CQ do, а другое - когда bo CQ - do - При этом оси вращения, задаваемые вектором г для каждой траектории поворотов, разные. [13]

Итак, приходим к результату: два последовательных малых поворота тела могут быть заменены одним результирующим поворотом с вектором поворота, равным геометрической сумме слагаемых векторов поворота; от перемены порядка поворотов результирующий поворот не меняется. [14]

При Nn / 2 частота импульсов в пачке может быть сколь угодно высокой, так как результирующий поворот поля не превышает я эл. [15]

Страницы: 1 2