Конечный поворот

Cтраница 2

Если ввести в рассмотрение вектор ф конечного поворота тела, направлен ный вдоль оси вращения и численно равный углу поворота ф, для последовательных конечных поворотов пра вило векторного сложения действовать не будет. [16]

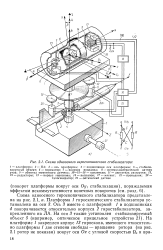Схема одноосного гироскопического стабилизатора. [17]

Оу стабилизации), пораждаемая эффектом некоммутативности конечных поворотов ( см. разд. [18]

Целесообразно попытаться установить соответствие между векторами и конечными поворотами, описываемыми ортогональными матрицами. Вектор, который мы поставим в соответствие некоторому повороту, должен, конечно, иметь определенное направление - направление оси вращения и определенную величину, например равную углу поворота. Мы сейчас увидим, что успешно осуществить такое соответствие оказывается невозможным. Предположим, что А и В будут двумя такими векторами, связанными с преобразованиями А и В. [19]

Приближенные зависимости для кривизн, кручения, вектора конечного поворота и деформаций эквидистантного слоя в рамках теории малых деформаций приведены в разделах 9.4.3 и 9.4.4, посвященных прикладным нелинейным теориям оболочек. [20]

Сравнительная простота и компактность настоящего изложения теории вектора конечного поворота достигнута за счет применения бескоордйнатных методов тензорного анализа. [21]

Оба последних утверждения не имеют места для рассмотренных ранее конечных поворотов, сложение которых происходит не по простым правилам векторного исчисления, а по правилам введенного Гамильтоном исчисления кватернионов. [22]

Последняя формула показывает, что результирующий поворот двух конечных поворотов твердого тела вокруг неподвижных осей зависит от порядка выполнения этих поворотов. [23]

В перечисленных классификациях вектор Ф и градиенты перемещений не описывают полностью конечные повороты материальных элементов оболочки при нелинейном деформировании. [24]

При перемещении вращающегося тела из одного положения в другое центр конечного поворота остается неподвижным. [25]

Наличие в ней слагаемого 62 X i указывает на некоммутативность конечных поворотов. [26]

В связи с этим еще раз подчеркнем, что для конечного поворота нельзя написать определение, аналогичное (4.10), так как конечный поворот некоммутативен, а сложение векторов должно быть коммутативной операцией. Поэтому вектор бесконечно малого поворота был обозначен d /, а не d % ( вектора % не существует. [27]

Наличие в последней формуле слагаемого с произведением 62X61 указывает на некоммутативность конечных поворотов. Заключение о некоммутативности поворотов верно в предположении, что оси слагаемых поворотов фиксированы в неподвижной системе отсчета. [28]

Значок k обозначает номер ориентации в момент t, которая получена путем конечного поворота. Выберем то значение k, для которой величина v принимает наимеямее возможное значение. Его и возьмем за истинный. Таким обрезом, ориентации в момент t7 и t определены единственным образом. [29]

Между тем при наличии бесконечно малой пластической деформации никаких оснований для такого конечного поворота не имеется. Поэтому в точке пересечения с границей пластической области обе ветви траектории напряжений должны иметь общую касательную. Отсюда следует, что если в определенной точке пограничной кривой принять F-Fl, то ординаты Fl и F функции напряжений в упругой и пластической областях должны удовлетворять условию F Ft во всех точках границы. [30]

Страницы: 1 2 3 4