Погрешность - восстановление
Cтраница 1
Погрешность восстановления для основной волны и ее гармоник является систематической ( она всегда отрицательна, см. рис. 1 - 9, и приводит к уменьшению восстанавливаемой амплитуды кривой), однако если высокочастотная составляющая вызвана шумом или помехами и не синхронна с основной волной, то и погрешность восстановления оказывается случайной и наблюдается в виде случайного разброса отсчетов. [1]
Уменьшение погрешности восстановления достигается применением специальных временных окон или дополнительной информации о текущем спектре. [2]
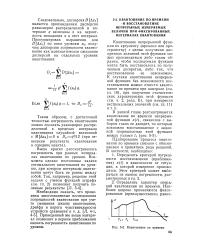 |
Квантование по времени. [3] |
Определить критерий погрешности восстановления ( приближения) x ( t) в зависимости от ситуации, в которой измерение производится. Этот критерий может выбираться из оценок погрешности, рассмотренных в гл. [4]
 |
Представление измеряемой функции x ( t степенными полиномами. [5] |
Зависимости между погрешностью восстановления, тактом измерения и значениями неучтенных пои восстановлении производных сигналов выведены в теории аппроксимации. [6]
Рассмотрим это свойство погрешности восстановления на конкрет ном примере. [7]
Будем считать, что погрешность восстановления подчиняется нормальному закону. [8]
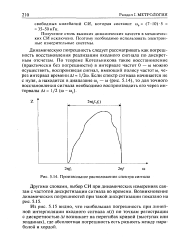 |
Произвольное расположение спектра сигнала. [9] |
Динамическую погрешность следует рассматривать как погрешность восстановления реализации входного сигнала по дискретным отсчетам. [10]
 |
Усиление случайной ного уравнения Абеля в слу-ошибки эксперимента в раз - чае точного задания функции личных методах решения урав -, . R МРТПТТР я Орнп. [11] |
Такая характеристика позволяет еще до реальной обработки эксперимента сделать оценки погрешности восстановления по максимуму ошибки измерений. [12]
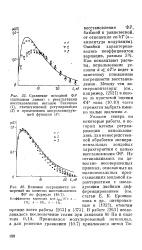 |
Сравнение исходной ФР ( сплошная линия с результатами восстановления методом Тихонова ( 1, статистической регуляризации ( 2 и применением аппроксимирующей функции ( 5. [13] |
Как показывают расчеты, использование условия d C kTle ведет к заметному повышению погрешности восстановления. [14]
Следовательно, значение погрешности в выражении (6.9) при оценке допустимого числа измерительных каналов должно определяться погрешностью восстановления наиболее быстродействующей функциональной зависимости. [15]
Страницы: 1 2 3