Подобраз
Cтраница 1
 |
Сверточный кодер со скоростью 2 / 3 для кодирования обоих информационных символов. [1] |
Подобразы D0, D2, D4 и D6 использованы как сигнальные точки с целью иллюстрации. Для восьми точечного созвездия каждый из подобразов С0, С, С2 и С3 содержит две сигнальные точки. Следовательно, пподобраз С0 содержит две сигнальные точки, соответствующие битам ( 000, 100) или ( 0, 4) в восьмеричной записи. Аналогично, С2 содержит две сигнальные точки, соответствующие битам ( 010, ПО) или ( 2, 6) в восьмеричной записи. [2]
 |
Решетка с 8 состояниями для прямоугольных сигнальных созвездий с КАМ. [3] |
Задание сигнальных подобразов для переходов основывается на том же наборе базовых ( эвристических) правил, описанных выше 8 ФМ сигнального созвездия. Параллельные переходы задают сигнальные точки, содержащиеся внутри соответствующих подобразов. Евклидово расстояние параллельных переходов превышает свободное евклидово расстояние и, следовательно, качество кода не ограниченно параллельными переходами. [4]
Информационные гены - элементарные подобразы, определяющие развитие и формирование сложных образов. [5]
Если образ можно описать с помощью иерархической структуры подобразов, аналогичной синтаксической структуре языка, то для решения задач распознавания образов применяют лингвистический ( или синтаксический) подход с использованием теории формальных языков. [6]
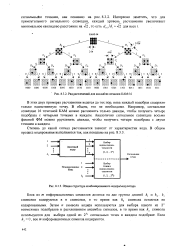 |
Ряд расчленений для ансамбля сигналов КАМ-16.| Общая структура комбинированного кодера / модулятора. [7] |
В этих двух примерах расчленения ведется до тех пор, пока каждый подобраз содерлсит только единственную точку. В общем, это не необходимо. [8]
Шестнадцатиточечное прямоугольное сигнальное созвездие показанное на рис. 8.3.2, сначала делится на два подобраза путем назначения альтернативных точек в каждом подобразе, как показано на рисунке. [9]
Шестнадцатиточечное прямоугольное сигнальное созвездие показанное на рис. 8.3.2, сначала делится на два подобраза путем назначения альтернативных точек в каждом подобразе, как показано на рисунке. [10]
Поскольку пропускная способность канала определяет окончательный предел качества кодирования, мы можем подчеркнуть, что непрерывное расчленение больших ансамблей сигналов быстро ведет к разделению сигнальных точек внутри некоторого подобраза, что расширяет свободное евклидово расстояние кода. В таких случаях параллельные переходы больше не являются ограничивающим фактором для DCB. Кодеры могут быть реализованы с обратной связью или без нее. Например, рис. 8.3.11 иллюстрирует три сверточных кодера без обратной связи, соответствующие решетчатым кодам с 4, 8, 16 состояниями для сигнальных созвездий 8 ФМ и 16 КАМ. [11]
Декодирование Витерби мягких решений для решетчато-кодированной модуляции выполняется двумя ступенями. Поскольку каждая ветвь решетки соответствует сигнальному подобразу, то - первая ступень декодирования сводится к определению наилучшей точки сигнала внутри каждого подобраза, то есть точку в каждом подобразе, которая ближе по расстоянию в к принятой точке. [12]
Процесс получения представления объекта включает в себя процедуры: а) разбиения ( сегментация) объекта; б) выделения признаков - непроизводных элементов. Чтобы найти представление объекта через его подобразы, необходимо его сегментировать и в результате этой операции идентифицировать ( выделить) его непроизводные элементы и действующие в объекте отношения между ними. Другими словами, объекты, прошедшие предварительную обработку, разбиваются на подобразы в соответствии с предварительно определенными синтаксическими операциями. Каждый подобраз, в свою очередь, отождествляется с некоторым заданным набором непроизводных элементов. В результате каждый объект получает свое представление с помощью некоторого набора непроизводных элементов и ряда фиксированных синтаксических операций. Например, при использовании операции соединения объект получает представление в виде некоторой цепочки соединенных непроизводных элементов. [13]
Подобразы D0, D2, D4 и D6 использованы как сигнальные точки с целью иллюстрации. Для восьми точечного созвездия каждый из подобразов С0, С, С2 и С3 содержит две сигнальные точки. Следовательно, пподобраз С0 содержит две сигнальные точки, соответствующие битам ( 000, 100) или ( 0, 4) в восьмеричной записи. Аналогично, С2 содержит две сигнальные точки, соответствующие битам ( 010, ПО) или ( 2, 6) в восьмеричной записи. [14]
Хотим указать на то, что специальное отображение кодовых символов в сигнальные точки, как иллюстрировано на рис. 8.3.1, где восемь сигнальных точек представлено в эквивалентную двоичную форму, существенно. Можно разработать иные отображения путем перестановки подобразов таким путем, чтобы сохранить основное свойство - увеличение минимального расстояния среди подобразов. [15]
Страницы: 1 2