Минимаксный подход

Cтраница 1

Минимаксный подход при суждениях, связанных с отысканием экстремума, не применяется. [1]

Минимаксный подход часто называется пессимистичным [27], ибо здесь расчет ведется исходя из наихудшей ситуации, когда потери достигают максимума. Противоположным Б этом смысле является миниминный критерий, когда наилучшей считается система, обеспечивающая минимум потерь в наилучшем случае. [2]

Минимаксный подход страдает известными недостатками, тем не менее применяется в теории статистических решений. Например, в игре, информация о которой приведена в табл. 24, согласно минимаксному подходу оба действия статистика равноценны ( это уже отмечалось в § 1, гл. [3]

Достоинством минимаксного подхода является то, что он не требует задания каких-либо произвольных функций. [4]

Обращаясь к минимаксным подходам, исследователи замечают, что ожидаемость наихудших сценариев может оказаться крайне низкой, и настраиваться на наихудший исход означает производить неоправданно высокие затраты и создавать необоснованные уровни всевозможных резервов. Компромиссным способом применения минимаксных подходов является использование метода Гурвица, когда два экстремальных сценария ( наихудший и наилучший) учитываются совместно, а в качестве веса в сценариях выступает параметр согласия /, уровень которого задается ЛПР. [5]

В некоторых случаях минимаксный подход приводит к практически неприемлемым решениям. [6]

Итак, при минимаксном подходе формируется некий класс ожидаемых сценариев развития событий в инвестиционном процессе, и из этого класса выбирают два сценария, при которых процесс достигает максимальной и минимальной эффективности соответственно. При / 0 ( точка Вальда) за основу при принятии решения выбирается наиболее пессимистичная оценка эффективности проекта, когда в условиях реализации самого неблагоприятного из сценариев сделано все, чтобы снизить ожидаемые убытки. Такой подход, безусловно, минимизирует риск инвестора. Однако в условиях его использования большинство проектов, даже имеющих реальные шансы на успех, будет забраковано. Возникает опасность паралича деловой активности с деградацией инвестора как лица, принимающего решения. [7]

В дальнейшем будем придерживаться минимаксного подхода (9.1.2), который не требует введения меры на классе задачи дает гарантированный результат. В качестве недостатка минимаксного подхода отметим, что он может приводить к слишком осторожному методу, ориентированному на наихудшие задачи из заданного класса В. Однако, сужая класс В, можно получать более эффективные минимаксные алгоритмы, ориентированные на более специализированные задачи. [8]

По сравнению с вероятностным подходом минимаксный подход обладает как некоторыми недостатками, так и рядом преимуществ. Минимаксная стратегия бывает иногда слишком осторожна, рассчитывая на наихудшую помеху. [9]

В качестве исходного пункта рассуждений возьмем минимаксный подход, оказавшийся весьма эффективным в случае, когда распределение w ( z x) известно, a w ( x) нет. [10]

Сделанные замечания говорят о том, что минимаксный подход следует применять с большой осторожностью. [11]

Существуют методы устойчивого оценивания, отличные от минимаксного подхода Хьюбера. [12]

Неопределенность формы распределения требует и в этом случае минимаксного подхода к определению уровня Х0; ограничения (6.9) - (6.12) сохраняют силу и в этом случае, но неравенство (6.18) позволяет ввести ограничения на вероятность р и тем самым снизить оценку верхней грани потерь. [13]

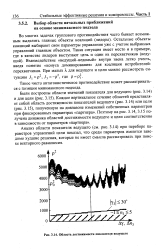Область достижимости показателя ведущего. [14]

Такое чисто антагонистическое противодействие может рассматриваться с позиции минимаксного подхода. [15]

Страницы: 1 2 3