Более простой подход

Cтраница 3

Непосредственный подход к этой задаче заключается в задании двух кодовых слов с помощью ортонормального разложения для L параллельных каналов, нахождении вероятности ошибки и затем оптимизации по кодовым словам. При более простом подходе следует заметить, что каждый из L каналов можно рассматривать как бесконечное множество гауссовских дискретных по времени каналов. Вероятность ошибки не может возрастать, если дисперсии шума в каждом множестве дискретных каналов уменьшаются до дисперсий для множества дискретных каналов с наименьшими дисперсиями. Это, однако, было бы равносильно использованию только лучшего множества каналов. [31]

Решение такого уравнения требует применения численных методов или счетно-решающей машины. Альтернативой является более простой подход в том случае, если точное знание формы переходного процесса не является необходимым, а желательно определить лишь интервал времени между некоторыми значениями выходного тока в переходном процессе. Основное предположение, которое делает проблему разрешимой, заключается в том, что все параметры транзистора, за исключением Спк, считаются линейными. [32]

Совместное квантовомеханическое рассмотрение системы взаимодействующих ионов и электронов приводит к не преодоленным до сих пор трудностям, в том числе и на основе вариационных методов. Поэтому обычно используется более простой подход, основанный на применении адиабатического приближения. В адиабатическом приближении ионы рассматриваются как классические частицы, движущиеся гораздо медленнее электронов, так что можно предполагать, что при каждом новом положении ионов электроны успевают придти в термодинамическое равновесие. [33]

Суть подхода заключается в том, чтобы отказаться от использования ASN. Expalin модели, а искали более гибкий и более простой подход с точки зрения реализации. В рамках InitResponse клиенту передаются описания ресурсов в виде XML описаний, которые в дальнейшем используются им для организации взаимодействия с сервером. XML описания могут быть доступны поисковым роботам интернет. [34]

Один из способов реализации сортировки методом Шелла заключается в том, что для каждого h независимо используется сортировка вставками на каждом из h подфайлов. Несмотря на очевидную простоту этого процесса, возможен еще более простой подход именно благодаря тому, что подфайлы независимы. [35]

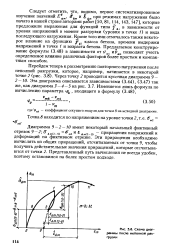Схема диаграммы после неполной разгрузки. [36]

Представленный путь вычисления не всегда удобен, поэтому остановимся на более простом подходе. [37]

Тэрстоуном ( Thu rstone, 1947), но в последнее время уже выяснилось, что не все его критерии формализуются в аналитическом виде. Поскольку Тэрстоун использует понятие гиперплоскости или подпространства, мы остановимся на более простом подходе Мьюлейка ( Mulaik, 1972), предполагающем знание лишь элементов теории векторных пространств. В определении Мьюлейка через г обозначено число общих факторов, а V - матрица вторичной структуры, образованная координатами ( нагрузками) вторичных факторов, получаемых в результате вращения. [38]

Таким образом, за исключением некоторых специальных случаев, дифференциальные уравнения ( VIII2) и ( VIII3) могут быть решены лишь с помощью двукратного численного интегрирования. Здесь будут рассмотрены только некоторые практически важные частные случаи, позволяющие использовать более простой подход. [39]

Определить точную величину поправки, учитывающей степень отклонения поверхности от абсолютно черной или идеально излучающей - задача весьма сложная для инженерного расчета. Однако, если можно допустить, что все поверхности серые, то возможен более простой подход к решению задачи. [40]

При этом скорость, масса и диаметр струи должны быть заданы. В некоторых случаях, при оценке среднего диаметра пробоины DO, на основе ряда допущений могут быть использованы более простые подходы, в которых можно получить аналитические или полу эмпирические зависимости диаметра пробиваемого в преграде отверстия. Он основан на рассмотрении энергетического баланса системы, при котором основная часть кинетической энергии КС затрачивается на необратимое пластическое деформирование материала преграды. При проникании элементов КС в преграду, ее кинетическая энергия расходуется на срабатывание самого г-го элемента струи в процессе проникания, на генерирование УВ, на разрушение материала преграды и его пластическое деформирование. При этом принимается, что каверна глубиной LI и переменным диаметром D ( рис. 17.296) образуется за счет того, что часть материала преграды разрушается и уносится в направлении поверхности преграды. Образованная при этом каверна имеет переменный диаметр по глубине вследствие влияния двух факторов: наличия свободной поверхности и неравномерного распределения кинетической энергии вдоль кумулятивной струи. Неравномерность в распределении кинетической энергии вдоль КС приводит к тому, что величина каверны по длине проникания меняется неравномерно. С учетом основного допущения можно записать, что ЕЛ aEwi, где ЕЛ - кинетическая энергия г-го элемента КС; EWI - энергия формоизменения деформируемой преграды при действии г-го элемента КС; а - коэффициент, учитывающий, какая часть энергии элемента струи расходуется на пластическое деформирование преграды, а также ряд других факторов. [41]

Рассмотрим теперь две группы методов нахождения точек вторичных вещественных бифуркаций. Эти методы, разумеется, пригодны и для нахождения точек первичной бифуркации, однако для этого случая выше описан более простой подход. Первую группу составляют разностные методы, тогда как методы второй группы основываются на методе стрельбы. [42]

При этом затухание определяется неупорядоченным движением атомов, рассматриваемых как свободные частицы. Последовательные усовершенствования подхода Власова были направлены на количественное улучшение этой картины, концентрируясь главным образом на процессах затухания, недооцениваемых в более простых подходах. [43]

Общее описание динамики течения дается уравнением Навье - Стокса [18] вместе с уравнением неразрывности. Однако для моделей с такой сложной геометрией, которые используются в хроматографии, решение системы этих уравнений практически невозможно, поэтому проводились поиски более простого подхода, основанного на аналогии между гидродинамикой к электродинамикой. [44]

Однако эта теория не может быть перенесена на многослойные спиральные канаты с центральной жилой. Так как многослойный спиральный канат представляет собой гораздо более сложную конструкцию, чем однослойный, то вопрос его расчета на первом этапе требует более простого подхода в пользу большей общности решения. Поэтому в предлагаемой статье задача рассматривается в более простой постановке, чем в работе [7], а именно: 1) внутренние силы трения между проволоками в расчет не принимаются; 2) канат предполагается достаточно обтянутым так, что технологические зазоры ликвидированы и ввиду наличия центральной жилы изменением его диаметра можно пренебречь. Эффектом Пуассона и контактным обмятием проволок, как это вытекает из работы Бендорфа [9], также можно пренебречь. Деформации проволок рассматриваются только в пределах упругости. [45]

Страницы: 1 2 3 4