Микроскопический подход

Cтраница 3

Теплообмен при кипении обычно изучают макроскопически, что позволило добиться определенных успехов, которые, однако, нельзя считать достаточными. При изучении пузырчатого кипения микроскопический подход обещает определенные выгоды. Величину коэффициента теплообмена при кипении в насыщенной жидкости можно считать известной, если мы знаем число центров парообразования и скорость роста пузырей. В настоящей статье рассматривается скорость роста пузырей в центрах парообразования. [31]

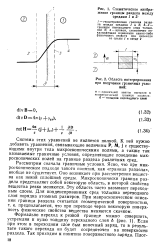Схематическое изображение границы раздела между средами 1 я 2.| Область интегрирования при получении граничных условии. [32]

Рассмотрим сначала граничные условия. Ясно, что при микроскопическом подходе такого понятия, как граница раздела, вообще не существует. Оно возникает при рассмотрении вещества как некой сплошной среды. Микроскопически граница раздела представляет собой некоторую область, в которой свойства вещества резко меняются. Эту область часто называют переходным слоем. [33]

Существует два различных подхода к расчету сил молекулярного взаимодействия. Первым по времени возникновения является микроскопический подход. Расчеты строятся на суммировании дисперсионных взаимодействий между отдельными молекулами. [34]

Используя модель упругой непрерывной среды, Дебай, конечно, понимал, что она применима только до тех пор, пока длина звуковой волны ( Л 2-тг / А) значительно превосходит межатомные расстояния. В случае коротких волн необходим микроскопический подход, основанный на исследовании колебаний атомов кристаллической решетки. В дальнейшем колебания молекул и атомов кристаллических решеток были тщательно изучены. Дебай, пытаясь предельно упростить задачу, выдвинул изящную идею. [35]

В то же время при микроскопическом подходе иногда удается описать всю эту сложную совокупность фазовых переходов на основе единого гамильтониана, содержащего 1 - 2 параметра. [36]

В термодинамике необратимых процессов дело обстоит существенно иначе. Однако ЛТР может быть рассмотрено лишь в терминах микроскопического подхода, что означает прежде всего следующее: для каждого достаточно малого, хотя все еще макроскопического объема фазового пространства отклонение распределения вероятностей микросостояний от гиббсовского распределения пренебрежимо мало. Там, где это не выполняется, возможен только статистический подход. Поэтому чисто макроскопическая теория необратимых процессов, по-видимому, не может быть построена. [37]

В нефтяных системах при соответствующих условиях возможны фазовые переходы, в результате которых формируются ССЕ различных размеров и состава. Исследование термодинамических зависимостей фазообразования в нефтяных системах возможно с позиций микроскопического подхода, в рамках которого рассматривается формирование единичной ССЕ. Термодинамический анализ показывает, что изменение размеров ССЕ в НДС под действием различных факторов носит экстремальный характер. [38]

Рассмотрение в ( 4) члена С вз, отвечающего за взаимодействие диффузных и колебательных типов движений, требует микроскопического подхода. В ней-тронодинамических опытах [6] обнаружено наличие в жидких металлах коллективных возбуждений. Нетрудно установить связь свойств симметрии среды металлических жидкостей с возможными типами коллективных возбуждений в них. Действительно, наличие ближнего порядка означает, что колебательные возбуждения ( фононы), с длиной волны порядка межатомных расстояний, могут распространяться лишь в пределах областей ближнего порядка ( ОБП) - это прямое следствие локального характера трансляционной симметрии в жидкости. [39]

При этом движение сверхтекучего гелия характеризуется одновременно двумя скоростями - сверхтекучей и нормальной, которые обе входят в уравнения движения. Микроскопический подход к сверхтекучему гелию основан на представлении о Квантуемых элементарных возбуждениях, которые образуют в жидкости своеобразный газ. Именно этому газу возбуждений обязано движение наличием второй - нормальной скорости. [40]

В этой главе излагаются основные сведения, необходимые для формулировки задач лазерной спектроскопии. Мы рассмотрим классическое описание полей излучения и квантовое описание среды. Основное внимание уделено микроскопическому подходу к связанным состояниям, в котором феноменологически учитываются различные физические процессы. Рассматриваемые физические явления весьма разнообразны, и многие из них лишь упоминаются. Некоторые утверждения не так просто обосновать и они часто основаны на эвристическом или прагматическом подходе. Пусть читатель не беспокоится, если те или иные аргументы поначалу покажутся ему неубедительными. Если основанные на них результаты и в дальнейшем не развеют сомнений, то работы, перечисленные в конце этой главы, помогут внести ясность. [41]

Результаты для отдельных частиц очень сходны с выводами для вмороженного потока. Но это разные задачи, хотя примененные при их решении методы очень похожи. Дело в том, что вмораживание потока является фундаментальным магнитогидродинамическим процессом, в котором плазма рассматривается как проводящая жидкость. Расчет для отдельных частиц является микроскопическим подходом, и, чтобы объединить эти два метода в один, надо показать, что можно выводить уравнения магнитогидродинамики из микроскопических уравнений движения. [42]

Совокупность границ, разделяющих различные физические состояния, или фазы, называется поверхностью или границей раздела. Одной и той же поверхности обычно принадлежат атомы различных кристаллических ( кристаллографических) плоскостей, характеризующихся различными кристаллографическими осями. Свойства каждой поверхности определяются не только присущим ей собственным порядком атомов, но и окружением, способным значительно влиять на ее характеристики. Таким образом, для описания свойств поверхности необходим микроскопический подход. [43]

Имеются два подхода к рассматриваемому вопросу. В этом пункте мы будем следовать изложению Дрейсера [ 871, при котором предполагается, что энергия газа изменяется со временем быстрее, чем происходит передача энергии между электронами и ионами и последней можно пренебречь. Это предположение соответствует условию д, использованному при микроскопическом подходе. [44]

Прослойка между двумя фазами. [45]

Страницы: 1 2 3 4