Фрактальный подход

Cтраница 2

Фрактальный подход, на наш взгляд, является лучшим основанием применения скейлинговых подходов для полимеров, нежели аналогия с магнетиками. [16]

Экспериментальные данные о распределении плотности взяты из работы [186], в которой анализируется конкретная производственная ситуация, связанная с тем, что плиты имеют дефект структуры, уменьшающий прочность на растяжение перпендикулярно к пласти в 3 раза по сравнению с требованиями ГОСТа. Используя фрактальный подход для анализа их структуры и прочности, можно заключить, что хотя плиты имеют допустимые значения интегральной плотности 690 - 705 кг / м3, аномально низкие значения фрактальной размерности макроструктуры D 2 67 и D 2 42 указывают на ее нарушение. Распределение прочности свидетельствует о том, что прочность внутренних слоев в 2 5 - 3 раза ниже допустимой. Таким образом, метод дает возможность непосредственно в технологическом потоке оперативно получать информацию о структуре, упругих, деформационных и прочностных свойствах древесностружечных плит. [17]

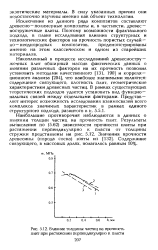Влияние толщины частиц на прочность плит при растяжении перпендикулярно к пласти. [18]

Исключение из данного ряда композитов составляют древесно - полимерные композиты и, в частности, древесностружечные плиты. Поэтому возможности фрактального подхода, в плане исследования влияния структурных и технологических факторов на прочность пористых случайно-неоднородных композитов, продемонстрированы именно на этом классическом и одном из старейших материалов. [19]

Зависимость плотности ленты от давления консолидации. [20]

Полученное в предыдущем параграфе уравнение состояния консолидируемой стохастической волокнистой среды позволяет перейти к исследованию проницаемости таких сред неньютоновскими жидкостями. Разрабатываемый в данной работе фрактальный подход дает возможность учесть влияние на коэффициент проницаемости среды ее неоднородности, а также процесса переформирования порового пространства при деформировании среды. [21]

В отличие от подхода, изложенного в работе [95], фрактальный подход позволяет получить зависимость скорости в полном диапазоне изменения пористости образцов. Из рисунка видно, что полученная теоретическая зависимость пересекает поле экспериментальных данных. [22]

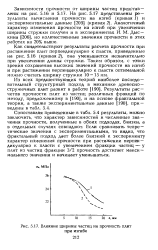Влияние ширины частиц на прочность плит при изгибе. [23]

Сопоставляя приведенные в табл. 5.4 результаты, можно заключить, что характер зависимостей и численные значения прочности, полученные в обоих подходах, близки, а в отдельных случаях совпадают. Если сравнивать теоретические значения с экспериментальными, то видно, что фрактальный подход дает более близкий к эксперименту характер изменения прочности при растяжении перпендикулярно к пласти с увеличением фракции частиц - у плит из частиц фракции 3 / 2 прочность достигает максимального значения и начинает уменьшаться. [24]

В теоретическом плане это связано с тем, что такие системы являются удобной модельной средой для описания эффективных характеристик материалов в рамках различных теоретических подходов, в том числе и методами теории перколяции. В данной главе на основе теории фракталов развивается более общий подход, позволяющий исследовать влияние процессов структурообразования на механические свойства композиционных материалов. Фрактальный подход к описанию структуры композиционных материалов дает возможность последовательно усложнять строение и набор рассматриваемых структур, что позволит позже перейти к описанию свойств таких сложных биокомпозитов, как натуральная древесина, древесно - полимерные композиционные материалы. [25]

В заключение можно отметить, что высказанные в [218] сомнения относительно возможности установления закономерности в поведении основной диаграммы краскопереноса ( рис. 7.26) на начальном участке имеют принципиальный характер. Как следует из данной работы, эта закономерность формируется в результате очень сложного по характеру взаимодействия микроструктуры бумаги и печатной краски. Вместе с тем полученные результаты свидетельствуют об эффективности использования фрактального подхода к проблеме исследования технологических проявлений давления печатного контакта. [26]

Одним из перспективных путей решения задачи количественного описания структур материалов, в том числе и сложной системы железо-углеродистых сплавов, является их параметризация, основанная на использовании теории фракталов. Для этого была введена фрактальная размерность, характеризующая в общем случае плотность заполнения объектом окружающего пространства, а также геометрические особенности этого заполнения. Однако если инструментальными методами невозможно определить внутреннее строение элементов структуры, либо имеется возможность получить снимок лишь локального участка структуры на одном масштабе, фрактальный подход для анализа не всегда применим. Преодоление этого ограничения связано с разработкой мультифрактального подхода, в частности, мультифрактальной параметризации ( МФП) структур. Проводить ее позволяет программа MFRDrom, созданная в ИМЕТ им. Она дает возможность на основе связи мультифрактальной и геометрической асимметрий вводить и исследовать количественные характеристики однородности и упорядоченности структур, которые извлекаются из плоских изображений с помощью компьютерного алгоритма. Применение МФП структур должно помочь в установлении местонахождения фуллеренов и доказательстве того, что на молекулярном уровне они необходимы для улучшения динамических свойств ( устойчивости, адаптивности) при диссипации энергии наряду с уже известными структурами адаптации. [27]

Поперечное сечение.| Микроструктура основного металла ( а, переходной зоны ( б. [28]

Существует множество интересных, на наш взгляд, явлений, которые лишь констатируются с позиций классической теории поверхности. Обзору этих проблем и посвящены первые четыре раздела данной главы. В разделе 4.3 приводятся обзор литературных данных и рассуждения о состоянии и свойствах реальных поверхностей с позиции теории фракталов. Мы считаем, что фрактальный подход к проблеме поверхностных явлений может явиться фундаментом для обобщения достигнутых результатов и прорыва в теории и научном понимании явления поверхности. [30]

Страницы: 1 2 3