Обычный подход

Cтраница 1

Обычный подход к такой проблеме заключается в том, что исследования с целью подбора подходящей, каталитической системы проводятся в три этапа. После разведочных ( поисковых) работ с различными типами соединений выделяют наиболее перспективные направления. Эти отобранные типы исследуются более систематически до получения результатов, удовлетворительных с точки зрения требований технологического и экономического анализа. Тогда полученные данные могут быть использованы для расчета и проектирования технологического процесса. [1]

Обычный подход требует организации четырех файлов: наименования деталей, наименования материалов, планового количества деталей и потребностей в материалах. [2]

Обычный подход к расчету ферм предусматривает замену распределенной произвольным образом нагрузки системой сосредоточенных сил, приложенных к узлам. В конечном итоге смещения ( и повороты в системах с жесткими связями), вызванные такой заменой, могут быть определены. Постановка задачи в матричной форме предполагает общее и систематизированное описание линейных стержневых систем, при этом решение сводится к последовательности повторяющихся вычислительных операций, хорошо приспособленных для реализации на вычислительных машинах. Как уже отмечалось выше, матричные методы неудобны для ручного счета. [3]

Обычный подход к расчету квазистационарного поля в пространстве, частично заполненном проводящей средой, состоит в отыскании решений уравнений поля в проводящих телах и в окружающей их воздушной среде и в склеивании этих решений с учетом краевых условий на поверхностях раздела сред. Основные математические трудности возникают при решении уравнений поля в проводящей среде, тогда как интегрирование уравнений поля в воздушной среде всегда можно свести к решению уравнения Лапласа. Поэтому заслуживают внимания те задачи, в которых можно обойти интегрирование уравнений поля в проводящей среде и свести весь расчет к решению уравнений поля во всем внешнем ( воздушном) пространстве. Приближенные краевые условия на границе проводящей среды можно ввести в тех случаях, когда проводящее тело является массивным и поверхностный эффект резко проявлен, либо когда проводящее тело представляет собой тонкую проводящую ферромагнитную оболочку. [4]

Обычный подход состоит в экспонировании пленки, неполном ее проявлении, засвечивании и окончательном проявлении. В общем это правильно, но требуется все делать по возможности точнее. [5]

Обычный подход к изучению неустойчивого состояния массообмена в дистилляционной колонне основан на упрощенном предположении, что перемешивание жидкости на каждой тарелке является полным, а жидкая фаза однородна по всей тарелке. Следовательно, эффективность дистилляционной тарелки принимается равной эффективности в любой отдельно взятой точке и постоянной в течение процесса массообмена. Однако такое предположение допустимо лишь при некоторых особых условиях, таких, какие имеются в малых колоннах или при выделении изотопов с небольшим изменением концентрации на тарелке. Для большинства же дистилляционных колонн это предположение не всегда имеет силу, й нельзя пренебрегать эффектом неполного перемешивания жидкости в переходном режиме. Таким образом, динамика эффективности тарелки может быть представлена в виде функции времени. Действительно, различные исследователи [4- 6] считают, что предположение о полном перемешивании жидкости может быть причиной расхождений между теоретическими и экспериментальными результатами. В Хьюстоне была разработана программа исследований с целью более основательного изучения динамики дистилляционных колонн. Конечная цель программы состоит в выявлении динамического соотношения между переменными процесса с тем, чтобы посредством этого соотношения перейти от рассмотрения эффекта неполного перемешивания жидкости на каждой отдельной тарелке к окончательному определению общего переходного процесса всей колонны. [6]

Обычный подход при их решении состоит в следующем. Ап) образует так называемое изображение ( га-мерный вектор), в отличие от образа, которому отвечает состояние машины или механизма. В га-мерном пространстве изображений образам соответствуют компактные области. Задача состоит в том, чтобы на основе той или иной меры сходства изображений определить эти области. Часто каждому образу ставится в соответствие эталонное изображение. Тогда исследуемое изображение сравнивается со всеми эталонами и относится к образу, чей эталон оказался ближе других в смысле выбранной меры сходства. [7]

Обычный подход, когда в конструкциях применяются демпфирующие устройства, позволяет оптимизировать систему только по максимуму демпфирования. В подобном подходе, хотя и правильном с точки зрения оптимального демпфирования, не учитывается то обстоятельство, что при присоединении к конструкции демпфирующих устройств или встраивании их в конструкцию могут изменяться и другие параметры, характеризующие формы колебаний. Поэтому зачастую оказываются существенными изменения всех трех параметров - коэффициента потерь, массы и жесткости - и следует попытаться оптимизм ровать демпфирующее устройство по всем трем параметрам, а не по одному из них. В зависимости от природы задачи и вида реакции конструкции следует оптимизировать различные параметры. [8]

Обычный подход к разрешению задачи определения норм амортизации как источника воспроизводства работающих машин, излагаемый в большинстве работ экономистов, состоит в следующем. [9]

Обычный подход в таких условиях состоит в приведении к единому времени затрат по вариантам и в их последующем сравнении с учетом ряда дополнительных ресурсных или иных ограничений. [10]

Обычный подход к этой проблеме сводится к утверждению о том, что у квантовой механики нет иного выбора, как постулировать сосуществование двух первичных и не сводимых друг к другу процессов: обратимой и непрерывной эволюции, описываемой уравнением Шредингера, и необратимой и дискретной редукции волновой функции к одной из входящих в нее собственных функций в момент измерения. Возникает парадокс: обратимое уравнение Шредингера может быть проверено лишь с помощью необратимых измерений, которые это уравнение, по определению, не может описывать. Следовательно, квантовая механика не может быть замкнутой теорией. [11]

Обычный подход к экологическому изучению жизненных циклов - сравнение их у двух или более популяций ( или видов, или групп) и попытка объяснить различия, исходя из особенностей сред обитания. Однако, как было показано, таксоны могут различаться и из-за того, что соответствуют разным точкам одной и той же аллометрической кривой, или из-за специфических эволюционных ограничений. Следовательно, экологические различия важно отделять от аллометрических и филогенетических. [12]

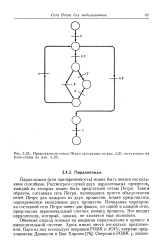Представление сетью Петри программы на, полученное из блок-схемы на. [13]

Обычный подход основан на введении параллелизма в процесс в вычислительной системе. [14]

Обычный подход к этой проблеме сводится к утверждению о том, что у квантовой механики нет иного выбора, как постулировать сосуществование двух первичных и не сводимых друг к другу процессов: обратимой и непрерывной эволюции, описываемой уравнением Шредингера, и необратимой и дискретной редукции волновой функции к одной из входящих в нее собственных функций в момент измерения. Возникает парадокс: обратимое уравнение Шредингера может быть проверено лишь с помощью необратимых измерений, которые это уравнение, по определению не может описывать. Следовательно, квантовая механика не может быть замкнутой теорией. [15]

Страницы: 1 2 3 4