Развитый подход

Cтраница 1

Развитый подход [6, 128] и полученное на его основе соотношение ( 84) позволяет учитывать влияние типа присоединения звеньев в цепи полимера на его температуру стеклования. [1]

Развитый подход дает, в частности, возможность решения статических задач о равновесном распределении намагниченности, в том числе и микромагнитных задач. [2]

Развитый подход имеет значение также и для пористых зерен сорбента, так как позволяет просто решить задачу о кинетике десорбции для тех случаев, когда JD - функция координаты, т.е. для различных неоднородных структур. [3]

Развитый подход на основе теории метода моментов имеет преимущество в том, что позволяет оценить влияние перепада давления на высшие моменты кривой. Кан [51] и Пето [38] рассмотрели роль динамической диффузии в капиллярной колонке, покрытой тонкой пленкой жидкой фазы. [4]

Развитый подход позволяет рассмотреть имеющий важное практическое значение вопрос о влиянии молекулярной массы полимера на его поверхностную энергию. [5]

Развитый подход, основанный на использовании метода стохастической аппроксимации, позволяет достаточно просто решать задачи идентификации сложных технологических объектов, описываемых системой дифференциальных уравнений первого порядка с частными производными. [6]

Развитый подход может быть обобщен на случай неизотермических реакций. Для этого необходимо лишь вместо величин dcj / dkq рассматривать величины dcj / dkljq и dcj / dEq, где k0q - пред-экспоненциальный множитель, Eq - энергия активации. [7]

Развитый подход отличают от ранее известных следующие характерные черты. Для точного решения задачи Римана здесь построен быстрый и эффективный численный алгоритм и получены оценки скорости сходимости итерационного процесса. При этом преодолена трудность, связанная с построением численного метода, который допускал бы сквозной расчет обмеления и областей сухого дна. Применение формул точного решения задачи Римана вместо формул приближенных решений по методам Куранта-Изаксона - Риса и Роу, включающих в себя операцию деления на квадратный корень из глубины ( разд. Таким образом, точное решение задачи Римана является более универсальным по сравнению с приближенными решениями, описываемыми далее. [8]

Развитый подход дает, в частности, возможность решения статических задач о равновесном распределении намагниченности, в том числе и микромагнитных задач. [9]

Таким образом, развитый подход позволяет находить эффективное решение обратных задач плоской теории упругости для любого числа отверстий и при любом их расположении. [10]

Отметим в заключение, что развитый подход может иметь приложение по крайней мере в двух аспектах. Прежде всего он позволяет непосредственно получить явное решение ряда оптимизационных задач, аналогичных описанной выше задаче о минимизации веса тепловой изоляции, обеспечивающей заданное тепловое сопротивление. С другой стороны, если установить строгие верхние или нижние оценки для фильтрационного расхода для класса областей заданной площади, эти методы могут быть использованы для оценки возможных фильтрационных расходов в тех случаях, когда форма области задана с некоторой неопределенностью, подобно другим качественным оценкам. [11]

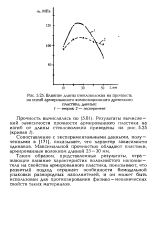Влияние длины стекловолокна на прочность на изгиб армированного композиционного древесного. [12]

Таким образом, представленные результаты, отражающие влияние характеристик волокнистого наполнителя на свойства армированного пластика, показывают, что развитый подход отражает особенности бимодальной упаковки разнородных наполнителей, и он может быть использован для прогнозирования физике - механических свойств таких материалов. [13]

Новый аспект теории экстракции комплексных кислот, связанный в начальной стадии с работами Сэлдика [38] и особенно Даймонда [39-40] и некоторых других авторов, базировался на привлечении теории растворов электролитов и закона действия масс. Развитый подход, особенно представление об эффекте общего иона, позволял объяснить зависимость коэффициента распределения металла от его концентрации, что, правда, в общих чертах делалось и ранее, и описывал влияние других сильных кислот, например хлорной. Соображения об ассоциации экстрагирующихся кислот ( HFeQ4, НАнС14) в растворителях с невысокой диэлектрической проницаемостью, высказанные и подтвержденные еще в ранних работах [17], были применены [42, 43] для объяснения явления соэкстракции. [14]

На основе модельных уравнений переноса для составляющих тензора напряжений Рейнольдса и турбулентного потока тепла, а также уравнений для турбулентной энергии и среднеквадратичных пульсаций энтальпии газовой смеси предложена методика самосогласованного расчета коэффициентов турбулентного переноса ( учитывающих в общем анизотропном случае различия интенсивностей турбулентных пульсаций состава, скорости и температуры вдоль разных осей координат) в зависимости от структурной характеристики флуктуации показателя преломления среды. Развитый подход основан в конечном счете на возможности определения внешнего масштаба турбулентности, как по градиентам осредненных термогидродинамических параметров течения многокомпонентной газовой смеси, так и по экспериментально определяемой структурной характеристике показателя преломления воздуха, с учетом его высотного распределения. Разработанная методика может найти применение в проекте непрерывного космического мониторинга озоно-сферы Земли путем зондирования атмосферы светом от эталонной звезды. В качестве основного статистического параметра зондирующей световой волны удобно для этих целей использовать, например, дисперсию флуктуации амплитуды, величина которой может быть рассчитана по измеряемому в эксперименте индексу мерцаний звезд. [15]

Страницы: 1 2