Закон - трансформация
Cтраница 2
Поэтому, в частности, симметричные четырехполюсники могут характеризоваться не только характеристиками, вытекающими из закона трансформации, но и коэффициентом отражения, измеряемым при подключении к линии волнового сопротивления. Преимущество последнего способа заключается в том, что коэффициент трансформации k и расстояние / от зажимов Гц трансформатора до входа четырехполюсника входят в одно и то же выражение. Поскольку формулы (27.14) и (27.15) очень просты, то практически безразлично, производятся ли вычисления с использованием коэффициента отражения или параметров закона трансформации. [16]
Если короткозамыкающнй поршень, расположенный вблизи точки С, находится в соответствующем разрыву положении, получается кривая закона трансформации. В противном случае координата у изменяется значительно сильнее. При приближении к точке разрыва лишь в отдельных небольших областях Q имеет место отклонение от кривой закона трансформации. [17]
Из проведенного рассмотрения также следует, что при перемещении реконструирующего источника законы трансформации восстановленного изображения будут аналогичны законам трансформации изображений с помощью линзы. В частности, продольное увеличение будет равно квадрату поперечного. [18]
Если речь идет о четырехполюсниках без потерь с выводами в виде линий, то графически, используя кривые закона трансформации отдельных четырехполюсников, можно найти кривую закона трансформации их последовательного соединения. Для произвольного положения ороткоза-мыкающего поршня х, включенного после четырехполюсника I, пользуясь кривой этого четырехполюсника, можно определить положение узла напряжения у. [19]
Таким образом, каждая плоскость, перпендикулярная оси х, рассекает поверхность шестиполюсника по кривой ( у, z) закона трансформации. [20]
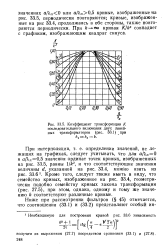 |
Коэффициент трансформации К последовательного включения двух линейных трансформаторов ( при. [21] |
Кроме того, следует также иметь в виду, что семейство кривых, изображенное на рис. 33.4, геометрически подобно семейству кривых закона трансформации ( рис. 27.5), при этом, однако, одному и тому же значению k соответствуют различные кривые. [22]
Если речь идет о четырехполюсниках без потерь с выводами в виде линий, то графически, используя кривые закона трансформации отдельных четырехполюсников, можно найти кривую закона трансформации их последовательного соединения. Для произвольного положения ороткоза-мыкающего поршня х, включенного после четырехполюсника I, пользуясь кривой этого четырехполюсника, можно определить положение узла напряжения у. [23]
То, что точка перегиба кривой Ci действительно находится в указанном месте, легко установить, используя рис. 27.5, согласно которому координаты двух точек одной и той же кривой закона трансформации ( абсциссы и ординаты) только тогда могут отличаться друг от друга на величину, равную четверти длины волны, если обе эти точки являются точками перегиба. В рассматриваемом примере в сечении I расположены зажимы трансформатора, соответствующие меньшему значению нормированного полного сопротивления. [24]
При этом не обязательно на отдельных кривых ( х, у) надписывать значения параметра г, удобнее рядом с основным семейством кривых, как это сделано на рис. 37.2, построить, например, кривую закона трансформации ( у, z) с хх0 0 25 в качестве параметра. [25]
Исключение составляет световой режим в глубине среды с т; 1, где его характер зависит только от свойств самой среды. В случае излучающих или люминесцирующих сред существенное значение приобретает закон трансформации излучения в акте его взаимодействия с диспергированной фазой или дисперсионной средой. [26]
С в известной точке Q, она определяется однозначно. Последнее утверждение мож о доказать, если наперед заданную кривую закона трансформации, проходящую через точку касания Q и точку Р, нанести на прозрачную бумагу, а затем наложить ее на семейство кривых закона трансформации ( рис. 27.5) и последнее смещать параллельно осям координат до тех пор, пока не будет найдена кривая семейства, проходящая через Р и Q. Используя этот прием, легко можно убедиться, что в действительности существует только одна такая кривая. Таким образом, для любого произвольного значения параметра z мож но однозначно построить соответствующую кривую закона трансформации ( х, у), а следовательно, и всю поверхность шестиполюсника. [27]
 |
Возможное распределение напряжения в линиях до трансформатора н после него.| Трансформация полного со противления устройством, изображенным на. [28] |
Таким путем можно, например, измерять полные сопротивления в волноводах, если в распоряжении имеется только коаксиальная измерительная линия и предварительно определены характеристики закона трансформации для соединительного элемента. [29]
Эквивалентная схема, изображенная на рис. 38Л, характеризуется шестью параметрами, а именно: координатами х, у, г точек I, II, III, расположенных на линиях L, L2, LZ, коэффициентами трансформации обоих трансформаторов Т и Г2 и реактивным сопротивлением JP. При определении этих параметров, исходя из характеристической поверхности шестиполюсника, следует воспользоваться тем, что положение уголков XQ, z / o, ZQ, кривая закона трансформации ( х, у), проходящая через точку ( д: 0 0 25; г / о 0 25), и кривая закона трансформации ( у, г) для параметра х ( хо 0 26) задаются этой поверхностью. И, наоборот, каждый построенный эквивалентный шестиполюс-ник однозначно определяет упомянутые элементы характеристической поверхности шестгаполюсника. Покажем теперь, что эти элементы полностью характеризуют всю поверхность шестиполюсника. Тем самым докажем, что построенная эквивалентная схема ( рис. 38.1) в отношении всех своих свойств соответствует заданному шестиполюс-нику. [30]
Страницы: 1 2 3