Закон - упрочнение
Cтраница 3
В этом случае к уравнениям равновесия, закона течения и условию текучести надо добавить уравнения неразрывности (1.6) и закона упрочнения (1.12), поскольку распределение плотности и параметра упрочнения должно быть определено в ходе решения. [31]
При Н ф 0 определяющие уравнения предлагаемой теории также являются уравнениями типа теории течения. В этом случае начальная поверхность текучести, представляющая в шестимерном пространстве напряжений Xi сферу радиуса К, в процессе пластического деформирования перемещается как жесткое целое, причем перемещение центра сферы пропорционально вектору остаточной ( пластической) деформации. Закон упрочнения, при котором начальная поверхность текучести испытывает перенос, сохраняя при этом свои размеры и форму, принято называть трансляционным упрочнением. Модель трансляционного упрочнения, аналогичная рассматриваемой в настоящей работе, была независимо несколько позднее предложена Прагером [82] для поверхности текучести общего вида. [32]
На основе конечноэлементной модели в предположении кусочно-линейных-поверхностей текучести и упрочнения дается матричное описание упругопластической системы. Рассматривается ее квазистатическое поведение при воздействии повторно-переменных нагрузок и дислокаций. Изучение охватывает широкий класс законов упрочнения, а также ситуаций, при которых изменения геометрии существенны для условий равновесия, о их влияние может быть выражено с помощью билинейных членов, содержащих исходные напряжения и дополнительные смещения. Установленная система положений предназначается в качестве основы для прикладной теории, характеризующейся высокой степенью общности. [33]
Пластическая деформация оказывает - достаточно существенное влияние на приведенный модуль g каждого из этих металлов. Однако результаты опытов этого параграфа показывают, что закон упрочнения для каждого из этих металлов устанавливается после первых 2 - 3 полу циклов и в последующем остается практически неизменным. [34]
Относительно малое число публикаций касается проблем учета физической нелинейности деформирования в контактных задачах. Значительно более подробно, с использованием различных критериев текучести [251, 267], законов упрочнения [60] и сложного характера нагружения [107, 112] рассмотрены задачи о внедрении штампов в упругопласти-ческие тела. Практически отсутствуют, за исключением работ [106, 166], решения контактных задач при наличии деформаций ползучести материала. [35]
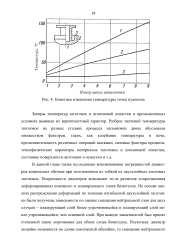 |
Кинетика изменения температуры точек пуансона. [36] |
В данной главе также исследовано возникновение погрешностей диаметров конических обечаек при изготовлении их гибкой из двухслойных листовых заготовок. Погрешности диаметров возникают из-за различия сопротивления деформированию основного и плакирующего слоев биметалла. На основе анализа распределения деформаций по толщине изгибаемой двухслойной заготовки были получены зависимости по оценке смещения нейтральной слоя для двух случаев - плакирующий слой более упрочняющийся и плакирующий слой менее упрочняющийся, чем основной слой. При выводе зависимостей был принят степенной закон упрочнения для обоих слоев биметалла. [37]
Точность любого критерия оценивается путем сопоставления результатов расчета и данных опыта. Известные экспериментальные дадшые о закономерностях деформирования и разрушения материалов при сложном напряженном состоянии весьма ограничены, что объясняется большими методическими трудностями при постановке опыта. Эти трудности значительно возрастают при проведении испытаний в условиях высоких и низких температур. По низко - и высокотемпературной прочности материалов при сложном напряженном состоянии в литературе опубликованы лишь качественные результаты, практически полностью отсутствуют какие-либо данные о принципах конструирования соответствующих испытательных средств. Этим вопросам во втором разделе уделено особое внимание. Здесь, в частности, подробно описаны методики и экспериментальные установки, разработанные и созданные в Институте проблем прочности АН УССР под руководством и при непосредственном участии авторов, проведен анализ основных экспериментальных результатов по изучению законов упрочнения и критериев предельного состояния наиболее типичных представителей отдельных групп конструкционных материалов в различных условиях механического и теплового нагружения. [38]
Страницы: 1 2 3