Показательный закон

Cтраница 3

У, убывают по равномерному показательному закону, тогда как решения, начинающиеся вдали от Y, растут подобным же образом. Этот тип поведения и проще по строению и богаче по свойствам, чем его обыкновенный аналог, как будет показано в этом параграфе и следующих главах. [31]

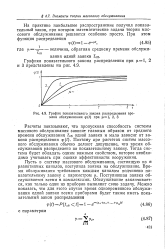График показательного закона распределения времени обслуживания p ( t при [ 11, 2, 3. [32]

На практике наибольшее распространение получил показательный закон, при котором математические задачи теории массового обслуживания решаются особенно просто. [33]

Важная роль, которую играет показательный закон времени обслуживания, связана с уже упоминавшимся свойством этого закона. Применительно к данному случаю оно формулируется следующим образом: если в какой-то момент происходит обслуживание требования, то закон распределения оставшегося времени обслуживания не зависит от того, сколько времени обслуживание уже продолжалось. [34]

Выявим одно весьма важное свойство показательного закона, состоящее в следующем. [35]

Так как колебания затухают по показательному закону, то теоретически они прекращаются только при оо. Но практически можно считать, что колебания прекратились, если амплитуда их упала до малой доли начальной величины. Обычно принято считать ( конечно, совершенно условно), что колебания затухли, если их амплитуда упала до 0 01 от начальной величины. [36]

Так как звук затухает по показательному закону, то время реверберации определяется условно, поскольку полностью звук затухает лишь при t со. [37]

Случайная величина Т распределена по показательному закону. [38]

Так как колебания затухают по показательному закону, то теоретически они прекращаются только при t оо. [39]

Если бы затухание происходило по показательному закону, то кривые на фиг. [40]

Дальнейшее повышение температуры происходит по показательному закону. [41]

Постоянный ток обычно нарастает по показательному закону ( фиг. [42]

Случайная величина X распределена по показательному закону с параметром К. [43]

Случайная величина X распределена по показательному закону с параметром К. [44]

Такие колебания называются затухающими по показательному закону. [45]

Страницы: 1 2 3 4