Полином - вид
Cтраница 1
Полиномы вида Рп ( х), F2n ( cp) являются полиномами системы функций Чебышева, так как не могут содержать более 2п корней, на любом рассматриваемом отрезке. [1]
Заметим, что гармонический полином вида ( I) имеет 2п 1 независимых коэффициентов. [2]
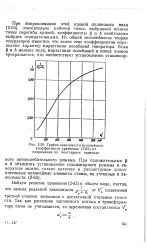 |
График зависимости нелинейного. [3] |
При аппроксимации этой кривой полиномом вида ( 2 - 63) относительно рабочей точки, ( выбранной вблизи точки перегиба кривой, коэффициенты р и 6 необходимо выбрать отрицательными. Из общей ( нелинейности теории генераторов известно, что знаки этих коэффициентов определяют характер нарастания колебаний генератора. [4]
Упражнение Доказать, что множество полиномов вида (5.4) ( где я предло-агается фиксированным, аь а2, а могт принимать любые вещественные значения) бразует лишенное пространство и это последнее является - мерным. [5]
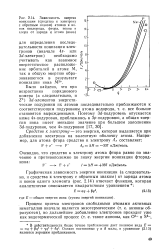 |
Зависимость энергии ионизации ( сродства к электрону с обратным знаком атомов и ионов кислорода, фтора, неона и хлора от заряда q атома ( иона. [6] |
В действительности более точное приближение дает полином вида Е aq р 2 у. Однако постоянные Y и 6 малы, и уравнение (2.13) является хорошим приближением. [7]
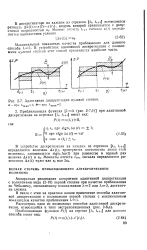 |
Адаптивная дискретизация нулевой степени. [8] |
Аппаратная реализация алгоритмов адаптивной дискретизации с полиномами вида ( 2 - 19) первой степени при качестве приближения по Чебышеву, оцениваемому показателями Я2 или К3, достаточна сложна. [9]
Прежде всего докажем, что пространство X полиномов вида х3 рх д без кратных корней гомотопически эквивалентно пространству У полиномов вида х3 ах2 Ьх с без кратных корней. [10]
Орбиты задаются условиями ju / co tat JV co-fiat Полиномы вида № ( 0, ) 1 / г [ Л находятся в инволюции. [11]
Для описания перемещений точек в срединной поверхности элемента задаются полиномы вида (6.20) ( без последних членов), а для радиальных перемещений - бикубический полином. Матрица жесткости получается 24-го порядка. [12]
Интерполятор четвертой степени обеспечивает проведение через пять опорных точек полинома вида, указанного в формуле ( 16), он построен по логической схеме, позволяющей избежать погрешностей обработки, возникающих в результате накопления ошибок округлений чисел конечных разностей. Этот интерполятор может обеспечить выдачу информации по кубичным и квадратичным параболам, а также линейную интерполяцию. [13]
Интерполятор четвертой степени обеспечивает проведение через пять опорных точек полинома вида, указанного в формуле ( 16), он построен по логической схеме, позволяющей избежать погрешностей обработки, возникающих в результате накопления ошибок округлений чисел конечных разностей. Этот интерполятор может обеспечить выдачу информации по кубичным и квадратичным параболам, а также линейную интерполяцию. [14]
Прежде всего докажем, что пространство X полиномов вида х3 рх д без кратных корней гомотопически эквивалентно пространству У полиномов вида х3 ах2 Ьх с без кратных корней. [15]
Страницы: 1 2