Полином - пятая степень
Cтраница 2
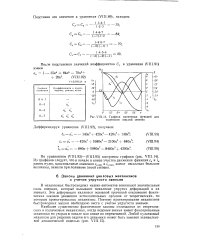 |
Графики единичных функций полиномов седьмой степени. [16] |
Из графиков следует, что в начале и конце участка движения функции ск и гк равны нулю, максимальные значения скшах и t KmaXj имеют несколько большие величины, нежели при полиноме пятой степени. [17]
Распределение скорости оказывается кубическим, т.е. таким же, как и в вертикальном слое между нагретыми до разной температуры плоскостями. Распределение температуры описывается нечетным полиномом пятой степени. Хотя в любом вертикальном сечении поперечная разность температур между плоскостями отсутствует, само течение приводит к формированию возле верхней и нижней границ слоев, внутри которых имеется потенциально неустойчивая вертикальная стратификация. Течение (30.2), (30.5) может быть реализовано в средней части протяженного в горизонтальном направлении слоя, торцы которого имеют разную температуру, а горизонтальные границы обладают высокой теплопроводностью. [18]
Соответствующая функция напряжений имеет форму полинома пятой степени. [19]
Если полученные результаты кажутся неудовлетворительными, лучшее приближение можно получить с помощью полинома четвертой степени, но это потребует некоторых дополнительных вычислений. Как будет показано в следующем разделе, можно найти такой полином пятой степени, который будет проходить фактически через все шесть заданных точек; в этом случае S принимает свое минимально возможное значение нуль. Но это, как указывалось в разд. [20]
На рис. 1.22 приведены кривые, характеризующие скорость сходимости каждой из аппроксимаций для значения максимального прогиба под силой. Из анализа их следует, что наилучшие результаты во всех случаях дает модель ( 5 - 5), использующая полином пятой степени для обоих перемещений. Модель с заданными деформациям ( 3 - D), подробно описанная в § 1.2, обладает высокими характеристиками во всем диапазоне изменения парамеров. Однако следует иметь в виде, что ее аналог для двумерных оболочек обладает существенным недостатком - несовместностью, который отсутствует в настоящем случае. Наихудшие результаты в всех случаях дает модель ( 3 - 1), что объясняется недостаточной точностью представления тангенциального перемещения. [21]
Для расчета консоли, нагруженной на конце сосредоточенной силой, оказалась подходящей функция напряжений в виде полинома четвертой степени, для свободно опертой по концам балки, находящейся под действием равномерно распределенной нагрузки - полином пятой степени. [22]
Эта формула показывает, что сравнительно небольшой ценой ( добавлением производных в двух конечных точках интервала) мы весьма значительно выигрываем в точности. Наше приближение теперь оказывается пятой степени. Это значит, что формула является точной для любой функции / ( х), которая может быть представлена каким-либо полиномом пятой степени. Правило Симпсона дает точные результаты лишь для полиномов третьей степени. В случае гладких функций две дополнительные степени создают большое увеличение точности. [23]
Эта формула показывает, что сравнительно небольшой ценой ( добавлением производных в двух конечных точках интервала) мы весьма значительно выигрываем в точности. Наше приближение теперь оказывается пятой степени. Это значит, что формула является точной для любой функции f ( x), которая может быть представлена каким-либо полиномом пятой степени. Правило Симпсона дает точные результаты лишь для полиномов третьей степени. В случае гладких функций две дополнительные степени создают большое увеличение точности. [24]
Линии же по этим точкам, имеющим обычно некоторый разброс, проведем после математической обработки полученных результатов. Для каждой характеристики методом наименьших квадратов найдем уравнение такой линии, которая наилучшим образом удовлетворяет экспериментальным точкам. Так как характеристика не описывается какой-либо простой функцией, представляя собой довольно сложную зависимость, будем искать линию, описываемую полиномом пятой степени. При этом, располагая 10 - 15 экспериментальными точками, мы получим, с одной стороны, довольно плавную линию - без излишних жзгибов, с другой стороны, эта линия пройдет довольно близко к экспериментальным точкам. [25]
На нескольких примерах было показано, как, выбирая решения плоской задачи в виде целых полиномов, можно получать распределение напряжений для изгибаемой полосы. Из полинома пятой степени получено решение для полосы, несущей равномерно распределенную нагрузку. [26]
Так, в работе [31] - приведены результаты изучения собственных поперечных колебаний тонких ортотроп-ных эллиптических пластинок с аналогичным эквидистантным вырезом. Теоретический анализ осуществлен с использованием метода Ритца. При этом проведено преобразование эллиптической пластинки в кольцевую с единичным внешним радиусом путем перехода к новой системе координат. Кольцевая круговая пластинка разбита на ряд секторов. Поперечные перемещения аппроксимируются рядами произведений приемлемых функций секториальнрй балки с малым углом конусности в плане на тригонометрические функции угловой координаты. Перемещения в направлении радиальной координаты аппроксимируются полиномами пятой степени, которые удовлетворяют основному уравнению изгибных колебаний балок. В результате проведенного исследования определены собственные числа и формы собственных колебаний для некоторых образцов изотропных эллиптических и круговых пластинок с подобными центральными вырезами. Для апробации полученных авторами результатов в работе дано сопоставление с результатами точных решений и результатами других авторов, полученных для частных случаев. [27]
Ввиду отсутствия некоторого общепринятого стандарта проверку погрешности какой-либо измерительной системы можно осуществить, выполняя измерения на таких материалах, параметры которых уже исследованы и результаты измерений для которых хорошо воспроизводятся. Наиболее широко для контрольных измерений скорости звука используется дистиллированная вода, иногда для этих целей применяется также физиологический раствор с известной концентрацией хлорида натрия. При проведении подобных измерений необходим строгий контроль за температурой среды. С другой стороны, контролируемое изменение температуры может служить удобным средством испытания измерительной системы в определенном диапазоне значений скорости звука. На рис. 5.2 представлены зависимости скорости звука от температуры для дистиллированной воды, физиологического раствора и различных смесей этилового спирта с водой. Дель-Гроссо и Мейдер [21] на основании обработки экспериментальных данных получили, что зависимость скорости звука в дистиллированной воде от температуры хорошо аппроксимируется полиномом пятой степени. Было показано, что такая аппроксимация позволяет рассчитать скорость звука в воде с точностью не хуже 0 015 м / с при нормальном атмосферном давлении в интервале температур ( Т) от 0 до 100 С. [28]
Страницы: 1 2