Полином - шестая степень
Cтраница 1
Первоначальный длинный полином шестой степени сведен к новому полиному лишь второй степени при точности, которая может оказаться достаточной во многих случаях. [1]
Он соответствует полиному шестой степени. Последним членом никак нельзя пренебречь. [2]
Он соответствует полиному шестой степени. [3]
Взяв, например, решение в виде полинома шестой степени и комбинируя его с решениями параграфа 14, мы можем получить напряжения в вертикальной консоли от нагрузки, изменяющейся по гидростатическому закону, как показано на фиг. [4]
В качестве примера пользования этими критериями приведем три различных полинома шестой степени, коэффициенты которых сведены в табл. П-7. Они все нормированы по свободному члену, поэтому вычисления упрощаются. [5]
Толлмиена к исследованию движения в диффузоре, аппроксимируя профиль скоростей в виде полинома шестой степени. [6]
V - l ( c) [ ] M, и это последнее множество состоит из конечного числа постоянных функций, так как V ( a) - полином шестой степени по переменной а. Так как ю ( ф) связно, то отсюда следует, что в ( ф) состоит из одной точки, и каждое решение уравнения (5.3.2) стремится к постоянной. [7]
На рис. 4 цифрой 1 показаны экспериментальные значения; 2 - сплайн-аппроксимация; 3 - производная от сплайна без сглаживания; 4 - производная при S 20; 5 - значения f ( x) при S 50; 6 - производная полинома шестой степени. [8]
В случае когда силы притяжения становятся очень малыми, А 0 и модель прямоугольной ямы переходит в модель жестких сфер. Результат представляет собой полином шестой степени Д с коэффициентами, не зависящими от температуры. [9]
Так, например, полином шестой степени дает возможность найти распределение напряжений для случая нагрузки, распределенной по закону треугольника. [10]
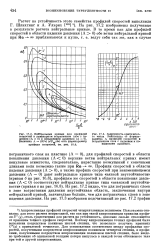
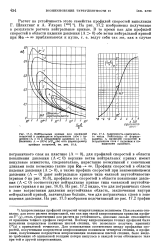
Аппроксимация профилей скоррстей четырехчленным полиномом Польгаузена оказалась для этого расчета непригодной, так как при такой аппроксимации кривизна профиля U ( г /), столь существенная для расчета на устойчивость, довольно сильно отклоняется от кривизны точного профиля скоростей. Поэтому аппроксимация точных профилей была выполнена посредством полинома шестой степени, что позволило получить кривизну U ( y) с приемлемой точностью. Для установления соответствия между профилями скоростей, полученными посредством аппроксимации полиномом четвертой степени, и профилями, полученными посредством аппроксимации полиномом шестой степени, было введено требование об одинаковой толщине потери импульса в каждой точке обтекаемого тела при той и другой аппроксимации. [12]
Например, с помощью функции напряжений в виде полинома шестой степени решается задача об изгибе консоли нагрузкой, изменяющейся по линейному закону. При нагрузке, изменяющейся по квадратичному закону подходит полином седьмой степени. [13]
Аппроксимация профилей скоррстей четырехчленным полиномом Польгаузена оказалась для этого расчета непригодной, так как при такой аппроксимации кривизна профиля U ( г /), столь существенная для расчета на устойчивость, довольно сильно отклоняется от кривизны точного профиля скоростей. Поэтому аппроксимация точных профилей была выполнена посредством полинома шестой степени, что позволило получить кривизну U ( y) с приемлемой точностью. Для установления соответствия между профилями скоростей, полученными посредством аппроксимации полиномом четвертой степени, и профилями, полученными посредством аппроксимации полиномом шестой степени, было введено требование об одинаковой толщине потери импульса в каждой точке обтекаемого тела при той и другой аппроксимации. [15]
Страницы: 1 2