Полином - шестая степень
Cтраница 2
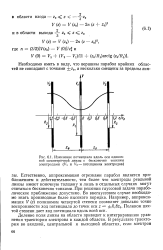 |
Изменение потенциала вдоль оси одиночной симметричной линзы с бесконечно тонкими электродами ( Ki и Vz - потенциалы электродов. [16] |
Естественно, аппроксимация отрезками парабол является приближением к действительности, тем более что электроды реальной линзы имеют конечную толщину и лишь в отдельных случаях могут считаться бесконечно тонкими. При решении гауссовой задачи параболическое приближение допустимо. Во внегауссовом случае необходимо знать производные более высокого порядка. Полином шестой степени дает ход потенциала вдоль всей оси. [17]
Практическое применение способа квадратичной аппроксимации при расчетах оптимальных сезонных режимов Волжско-Камского каскада в составе шести ГЭС показало, что на ЦВМ Урал-4 квадратичная аппроксимация характеристик шести ГЭС в десяти расчетных интервалах требует меньше 1 мин машинного времени. Характеристики ГЭС, представленные квадратичным полиномом, в широком диапазоне хорошо согласуются с фактическими характеристиками. На протяжении всего оптимизационного расчета повторять квадратичную аппроксимацию требуется не более трех-четырех раз. Таким образом, суммарные затраты машинного времени на последовательную квадратичную аппроксимацию характеристик ГЭС оказались весьма малы. Достигаемый от квадратичной аппроксимации эффект хорошо иллюстрируется следующим элементарным подсчетом. Квадратичный полином от двух переменных вычисляется быстрее полинома четвертой степени более чем в 2 раза, а квадратичный полином от одной переменной вычисляется быстрее полинома шестой степени более чем в 2 / 2 раза. Эти цифры показывают, что применение последовательной квадратичной аппроксимации характеристик ГЭС существенно сокращает машинное время решения всей оптимизационной задачи. [18]
Страницы: 1 2