Полином - тип
Cтраница 1
Полином типа ( 10) позволяет выявить влияние каждого отдельного фактора и совместное их влияние. Степень влияния каждого фактора на функцию отклика легко устанавливается, если рассчитать уравнение регрессии при последовательном исключении факторов хх, хг, хв. [1]
Полиномы типа У аналогичны полиномам типа X. [2]
Задачу с полиномом типа Rn ( х) с диапазоном ( 0; 1) предоставим учащемуся решить самостоятельно. [3]
Хъ, Х4 - полиномы типа (1.23); Vit V2, PI, Ps - перемещения вдоль оси у и углы поворота относительно этой же оси в начале и конце стержня; W, Wa, YI, Ys - перемещения вдоль оси z и углы поворота относительно этой же оси в начале и конце стержня. [4]
Полиномы типа У аналогичны полиномам типа X. [5]
Отсюда видно, что аппроксимация логарифмической амплитуд-ночастотной характеристики полином типа (6.63) и фазочастотной характеристики полином типа (6.64) позволяет оценить кумулянты &, а следовательно, моменты весовой функции. [6]
Если окажется, что 8 % А, то соответствующий полином типа ( V - 41a) может рассматриваться как математическая модель сложного объекта. [7]
Задача определения вектора а заранее не заданной размерности k полинома типа ( V-40) является, как было показано ранее, неустойчивой в эвклидовой метрике. [8]
Отсюда видно, что аппроксимация логарифмической амплитуд-ночастотной характеристики полином типа (6.63) и фазочастотной характеристики полином типа (6.64) позволяет оценить кумулянты &, а следовательно, моменты весовой функции. [9]
Разумеется, что правые части уравнений ( 156) могут содержать вместо коэффициентов передачи полиномы типа Pt ( р ], означающие введение производных от входных величин. [10]
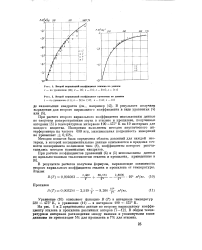 |
Второй вириалышй коэффициент этилена по данным.| Второй вириальный коэффициент пропилена по данным. [11] |
Методом попыток была определена область давлений для каждой изотермы, в которой экспериментальные данные описываются в пределах точности эксперимента полиномом типа ( 8), коэффициенты которого рассчитывались методом наименьших квадратов. [12]
Тем не менее, если не пытаться удовлетворить уравнению ( 2 32) точно, то функцию распределения в виде полиномов типа (2.48) можно с успехом использовать для отыскания решения в среднем с помощью метода моментов. [13]
Здесь мы изложим некоторые факты из теории инвариантов Васильева, развитой в работах Васильева, Бар-Натана, Бирман, Лина и Концевича и красиво объясняющей аддитивные свойства полиномов типа Джонса. [14]
Наряду с такого рода локальным определением деформаций возможно и определение деформаций как непрерывных функций координат. Для этого полиномы типа (2.7), (2.15) строят на достаточно большой области, а затем по формулам (1.26), (1.28), (1.38) рассчитывают деформации. [15]
Страницы: 1 2