Операторный полином

Cтраница 2

Анализ характеристического уравнения ( 581) показывает, что в качестве характеристических уравнений систем могут быть приняты операторные полиномы, полученные при развертывании главных определителей А систем автоматического регулирования, если в них оператор принять за некоторую искомую алгебраическую величину. [16]

Вид характеристического уравнения ( 247) показывает, что впредь в качестве характеристических уравнений систем могут быть приняты операторные полиномы ( 227), ( 229), ( 235), ( 239) и др., полученные при выводе уравнений движения систем регулирования, если оператор в них р принять за некоторую искомую алгебраическую величину. [17]

Вид характеристического уравнения ( 624) показывает, что впредь в качестве характеристических уравнений систем могут быть приняты операторные полиномы ( 515), ( 529), ( 534), ( 564) и др., полученные при развертывании главных определителей А систем автоматического регулирования, если оператор р принять в них за некоторую искомую алгебраическую величину. [18]

Это решение совпадает с решением уравнения ( 11), что и должно было быть, поскольку умножение на операторный полином является эквивалентным преобразованием. [19]

ДА /, должен соответствовать свободному члену дифференциального линеаризированного уравнения, в котором в качестве коэффициента при Дл имеется операторный полином наивысшей степени. [20]

Очевидно, что в случае, когда система обладает сосредоточенными постоянными параметрами, передаточная функция представляет собой отношение двух операторных полиномов. [21]

Переменные р, ф и г) - углы дрейфа, крена и рыскания соответственно; ац ( ij) - основные операторные полиномы каналов объекта регулирования; uij ( iV /) - операторы межканальных физических взаимосвязей объекта; & н - координата руля поворота; ft - возмущающие воздействия; hit, Ьц - постоянные коэффициенты, причем btj ( iV /) характеризуют неавтономность органа управления. [22]

Знаменатель A ( D) передаточной функции W ( D) называется характеристическим операторным полиномом, а числитель В ( D) - входным операторным полиномом. [23]

Дифференциальное уравнение D ( p) XU ( p) y ( t), гдеО ( р) кИ ( р) - операторные полиномы, представляет линейное неоднородное дифференциальное уравнение с произвольной заданной функцией времени в правой части. [24]

Если имеется другая последовательность полиномов, также равномерно сходящаяся к ф ( /) ( в т, М ]), то последовательность соответствующих операторных полиномов будет сходиться к тому же предельному оператору, что и первоначальная последовательность. В этом можно убедиться, объединяя обе последовательности в одну. [25]

Против примера с уравнениями ( 33) - ( 35) и ( 25) - ( 26), когда система уравнений, сохраняющая устойчивость при достаточно малых вариациях любых коэффициентов, переходит после эквивалентных преобразований в систему, способную терять устойчивость при сколь угодно малых вариациях, выдвигалось следующее возражение: поскольку при преобразованиях использовалась операция дифференцирования, то причина потери устойчивости может заключаться в том, что в ходе преобразований произошло умножение на негурвицев операторный полином. [26]

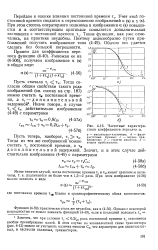Частотные характеристики коэффициента передачи ос. [27]

При этом степень операторного полинома в изображении a ( s) повышается и в соответствующем оригинале появляется дополнительная экспонента с постоянной времени тг Такие функции, как уже отмечалось, на практике неудобны. Обычно это удается сделать без большой погрешности. [28]

Затруднения указанного характера легко объясняются и преодолеваются с позиций метода коэффициентов преобразования. При этом состояние равновесия рассматривается как следствие почленного приравнивания операторных полиномов коэффициентов преобразования, что порождает ряд уравнений равновесия и позволяет определять не только два, но и большее число неизвестных параметров. Такое состояние равновесия частотнонезависимо и обусловлено совмещением частотных характеристик сравниваемых в СУ активных величин. Оно может быть опознано различными способами, например, изменением частоты питания схемы. [29]

До момента возмущения автоматическое устройство или система может находиться в состоянии покоя, что отвечает нулевым начальным условиям. Передаточная функция при нулевых начальных условиях может быть записана просто отношением операторных полиномов входной и выходной величин звена или системы. [30]

Страницы: 1 2 3