Приведенный полином

Cтраница 1

Конкретные приведенные полиномы, отображающие пять вышеуказанных случаев и соответствующие им контурные кривые для отклика у ( сплошные линии), а также для отклонения от линейности у. [1]

Задан приведенный полином Р от не более чем пяти переменных. [2]

Коэффициенты приведенных полиномов получают, используя свойство насыщенности плана. [3]

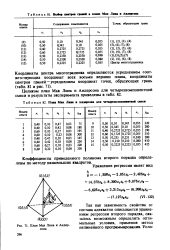Выбор центров граве плаве Мак Лвш в Авдерсова.| Плав Мак Лвва в Андерсона для четырехкомповевтвов смеем.| План Мак Лина и Андерсона. [4]

Коэффициенты приведенного полинома второго порядка определены по методу наименьших квадратов. [5]

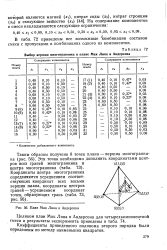Выбор вершин многогранника в плане Мак Лина и Андерсона.| План Мак Лина и Андерсона. [6]

Коэффициенты приведенного полинома второго порядка были определены по методу наименьших квадратов. [7]

По заданному приведенному полиному построить другой приведенный полином, который является производной исходного по заданной переменной. [8]

Нелинейная часть приведенных полиномов называется синергизмом, если она вызывает превышение отклика по сравнению с откликом, предсказываемым линейной частью, и антагонизмом - в противном случае. [9]

Степенью одночлена приведенного полинома назовем сумму показателей встречающихся в нем переменных. Переставляя одночлены заданного приведенного полинома, добиться, чтобы они были упорядочены в соответствии с ростом их степеней. [10]

По двум заданным приведенным полиномам построить третий полином, который является произведением двух исходных. [11]

По двум заданным приведенным полиномам от одной переменной определить, делится ли первый полином на второй без остатка. [12]

Для оценки коэффициентов приведенного полинома (4.2) в [41] были предложены планы, обеспечивающие равномерный разброс экспериментальных точек по ( q - 1) - мерному симплексу. [13]

Изолинии для симплекс-решетчатых планов второго ( а, неполного третьего ( б, третьего ( в и четвертого ( г порядков. [14]

Так как число коэффициентов приведенного полинома точно соответствует числу точек симплексной решетки ( план насыщен), для проверки полученной математической модели на адекватность отображения экспериментальных результатов необходимо проведение одного или нескольких дополнительных проверочных опытов. [15]

Страницы: 1 2