Данный полином

Cтраница 1

Данные полиномы таковы, что при насыщенности 5 0 76 ( S 0 76) фазовая проницаемость для газовой фазы равна нулю, ki 0, а при 5: 30 5 ( S 0 5) фазовая проницаемость для жидкой фазы больше нуля, &20. [1]

Данный полином удовлетворяет однородному дифференциальному уравнению изгибаемой пластины. [2]

Гурвица данного полинома равны нулю. Тем не менее среди его нулей z - - a j / 3, 2: 3 4 % j / З два нуля являются правыми. [3]

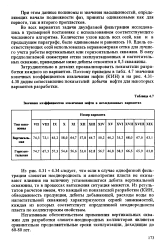Значения коэффициентов извлечения нефти в исследованных вариантах. [4]

При этом данные полиномы и значения насыщенностей, определяющих начало подвижности фаз, приняты одинаковыми как для первого, так и второго пропластков. [5]

Семейство ц-полустабилъных пучков с данным полиномом Гильберта Р ограничено. [6]

Чтобы проверить, является ли данный полином А ( р) полиномом Гурвица, его представляют в виде суммы полиномов с четными и нечетными степенями. [7]

Итак, рассмотренный метод позволяет определить, является данный полином полиномом Гурвица или нет. Он заключается в следующем. [8]

Являются ли эти свойства достаточными для того, чтобы утверждать, что для данного полинома Д ( я, у) найдется зацепление, полиномом которого он является, неизвестно. [9]

Для доказательства равенств ( 151) и ( 152) достаточно проверить, что данные полиномы ортогональны с одинаковым весом, и сравнить коэффициенты при старшей степени. [10]

Это, как известно, всегда возможно, так как для 2га неизвестных коэффициентов данного полинома имеем систему 2га уравнений, получаемых из ( 10 23), определитель которой Ап отличен от нуля. [11]

Для всякого устойчивого полинома степени п 1 существует устойчивый полином степени п, для которого данный полином является присоединенным. [12]

Доказать, что пространство полиномов К [ х ] есть прямая сумма пространства полиномов, делящихся на данный полином ср 6 К [ х ], и пространства полиномов, степени которых меньше степени ср. [13]

Это означает, что найденное значение х на стороне ортогона Ог02, соответствующее этому положению, и является одним из искомых вещественных корней данного полинома. [14]

Следующая лемма утверждает, что для любых у 1 полиномов от v переменных существует нетривиальный полином оти 1 переменных, тождественно равный нулю на данных полиномах. [15]

Страницы: 1 2