Данный полином

Cтраница 2

Функция Ф отличается от Ф тем, что в сумму, стоящую в знаменателе функции Ф, не включаются слагаемые е с номерами i, совпадающими с номерами узлов интерполирования для данного полинома, так как в узлах значения функции у / ( х) и полинома L ( х) равны между собой. Функция Фх предъявляет повышенные требования к точности интерполирования в промежутках между узлами. Ею целесообразно пользоваться при аппроксимации именно интерполяционными полиномами. [16]

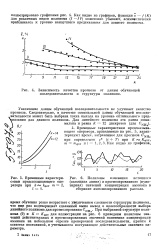Зависимость качества прогноза от длины обучающей последовательности и структуры полинома.| Временные характери - [ IMAGE ] 6. Полигоны изменения истинного. [17]

Как видно из графиков, функции е, - / ( К) для различных видов полинома ( / - IV) монотонно убывают, асимптотически приближаясь к уровню наилучшего предсказания для данного полинома. [18]

Если функция / ( х) задана таблично и аналитическое выражение ее неизвестно, то оценка погрешности интерполяционного полинома, строго говоря, является невозможной. Действительно, для данного полинома теоретически можно построить бесчисленное множество различных функций, совпадающих с этим полиномом в данной системе узлов. Таким образом, в промежуточных точках отклонение интерполяционного полинома от функции может быть каким угодно. [19]

Сейчас изучим задачу минимизации числа умножений, необходимых для вычисления одного полинома, когда разрешается представлять полином любым множеством параметров, вычисляемых по коэффициентам. Если бы нам было нужно вычислять данный полином несколько раз, то разумно было бы потратить некоторое время на вычисление другого представления полинома, при условии что новое представление даст более быстрое вычисление. [20]

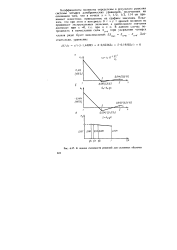К оценке сходимости решений для сплошных оболочек. [21]

Коэффициенты полинома определены в результате решения системы четырех алгебраических уравнений, полученных на основании того, что в точках х 1, 1 / 2, 1 / 3, 1 / 4 он принимает известные, приведенные на графике значения. Покажем, что при этом в интервале 0 х данный полином не принимает экстремальных значений, а наибольшего значения достигает при х 0, т.е. при п оо. [22]

Увеличение длины обучающей последовательности не улучшает качество прогноза. Следовательно, в качестве оптимальной длины обучающей последо - tBaienbHOCTH может быть выбрана точка выхода на уровень оптимального предсказания для данного полинома. [23]

Одному и тому же полиному h ( p) соответствует несколько функций алгебры логики: функции, для которых числа Cm ( f) ( см. (10.1)) совпадают, дают одинаковые полиномы. Когда мы говорим, что некоторому полиному отвечает самодвойственная функция, это означает, что среди функций алгебры логики, соответствующих данному полиному, имеется самодвойственная. [24]

Если ввести переменную г - exp ( - jftre), то частотный коэффициент передачи трансвер-сального фильтра Н8 ( о) [ выражение (8.6) 1 можно представить в виде полинома по степеням z, который характеризуется своими нулями. Так называются значения z, в общем случае комплексные, в которых данный полином обращается в нуль. Вначале синтезируют трансверсальный фильтр с линейной фазовой характеристикой и находят соответствующие нули. [25]

В этом примере описан относительно простой метод проверки полинома на примитивность. Для проверяемого полинома нужно составить регистр LFSR с контуром обратной связи, соответствующим коэффициентам полинома, как показано на рис. 8.8. Затем в схему регистра следует загрузить любое ненулевое состояние и выполнять за каждый такт правый сдвиг. Если за один период схема сгенерирует все ненулевые элементы поля, то данный полином с полем GF ( 2) будет примитивным. [26]

Практически не бывает такого случая, чтобы номиналы пассивных элементов и параметры активного элемента точно соответствовали расчетным значениям. Как правило, они лежат в некотором интервале допусков, границы которого различны в зависимости от характеристик технологического процесса и, кроме того, могут изменяться ( обычно в сторону расширения) в процессе эксплуатации устройства вследствие изменения окружающей среды и внутренних процессов в элементах схемы. Другими словами, схема чувствительна к изменению номиналов и параметров элементов, причем степень чувствительности определяется целым рядом факторов, в том числе порядком аппроксимирующего полинома, порядком звеньев, реализующих множители данного полинома, типом схемной реализации. [27]

Основываясь на определениях, введенных в предыдущем абзаце, нам необходимо найти распределение всех корней полинома p ( s), прежде чем мы сможем сказать, является ли полином p ( s) полиномом Гурвица или модифицированным полиномом Гурвица. Известно, что определение всех корней полинома - задача непростая. Следовательно, непосредственно пользоваться определениями полинома Гурвица или модифицированного полинома Гурвица нежелательно. В этом разделе мы опишем методы, пользуясь которыми можно определить, является ли данный полином полиномом Гурвица или модифицированным полиномом Гурвица, не находя его корней. [28]

Страницы: 1 2