Понятие - зависимость
Cтраница 1
Понятие зависимости или независимости случайных величин является одним из важнейших понятий теории вероятностей. [1]
Вообще понятие вероятностной зависимости включает в себя зависимости всех числовых характеристик условных распределений одной случайной величины от значений другой случайной величины. [2]
Аналогичным образом определяется понятие зависимости от действия. [3]
При построении сетевого графика используется понятие зависимости в том случае, когда для нача работы требуется завершение другой, которую графически нельзя свести к начальному событию пер понятие необходимо для отображения всей структуры взаимосвязи работ. [4]
Гораздо сложнее обстоит дело с понятием зависимости случайных величин: если при изменении х изменилось у, мы не можем сразу сказать, является ли это изменение результатом зависимости от х или оно обязано лишь влиянию случайных факторов. Правда, и между случайными величинами может существовать строгая функциональная зависимость, устанавливаемая логическим путем. Подобного рода зависимость между случайными величинами обычно известна из теоретических соображений заранее, до всяких наблюдений. На практике она проявляется в том случае, когда для вычисления двух случайных величин используются одни и те же наблюдения ( случай косвенных измерений), например, при нахождении числа мужчин и женщин на 1000 человек населения или при вычислении площади квадрата по измеренной стороне. Если же для вычисления каждой из случайных величин используются свои наблюдения, то на эти случайные величины действуют разные случайные факторы, и функциональная зависимость между ними уже невозможна. [5]
Таким образом, исходным понятием является понятие зависимости. Если есть некоторая зависимость между переменными х и у, которая позволяет выразить у как функцию от х и х как функцию от у, то эти две функции и являются взаимно обратными. [6]
Таким образом, из следствия 1 вытекает, что понятие зависимости и независимости событий взаимно. [7]
Заметим, что существует несколько более общий подход к понятию зависимости функций, позволяющий построить глобальную теорию этого вопроса, однако мы не будем на этом останавливаться. [8]
Это является первым доказательством зависимости комплексообразования от природы радикала, которая расширяет понятие зависимости комплексообразования от величины молекулы триалкилалюминия. В данном случае это связано с тем, что триизобутилалюминии практически мономерен и энергия ассоциации его очень мала. Благодаря этому отпадает необходимость прибавления энергии расщепления ( 10 ккал) к энергии решетки щелочного галогенида, введенной при рассмотрении энергетической характеристики комплексов. [9]
При увеличении размерности входного вектора ( Р ( Х) К) для поиска несвязных сомножителей ( 7, удовлетворяющих ограничениям Р ( Х) К, для описания ситуаций нарушения детерминированности вводится понятие зависимости пары внутренних состояний от входной переменной и существенной зависимости переменных автомата. [10]
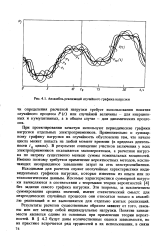 |
Ансамбль реализаций случайного графика нагрузки. [11] |
Результаты расчетов существенным образом зависят от того, связаны или нет между собой индивидуальные нагрузки. Понятие зависимости является одним из основных при применении теории вероятностей. [12]
БАЗИС множества X - минимальное порождающее его подмножество В. Это понятие связано с понятием зависимости: элементы X посредством операций из Q ставятся в зависимость от элементов В. В не порождается остальными его элементами. [13]
Интересно, что триизобутилалюминий А1 [ СН2СН ( СН3) 2 ] 3 по своим свойствам приближается к трипропилалюминию, а не к. Это является первым доказательством зависимости комплексообразования от природы радикала, которая расширяет понятие зависимости комплексообразования от величины молекулы триалкилалюминия. Благодаря этому отпадает необходимость прибавления энергии расщепления ( 10 ккал) к энергии решетки щелочного галогенида, введенной при рассмотрении энергетической характеристики комплексов. [14]
В регрессионном анализе при переходе от стохастических связей к причинным меняется лишь интерпретация результатов. В большинстве работ по теории вероятностей понятие независимости вводится аналитически, и из определений ясно, что два любых события, стохастически независимых, являются в то же время причинно независимыми. Само же понятие зависимости ( взаимозависимости, коррелированности, связи) вводится как отрицание независимости. [15]
Страницы: 1 2